Exponential functions and logarithms: Exponential functions
 The exponential function exp(x)
The exponential function exp(x)
The base e
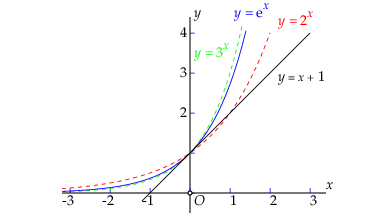
Between the base \(a=2\) and the base \(a=3\) there exist exactly one base, which we denote as \(e\), such that the graph of \(f(x)=\e^x\) and the straight line with equation \(y=x+1\) touch each other in the point \((0,1)\), i.e., where the graphs have exactly one point in common.
The value of this number is approximately \(2.71828\).
The exact value can be introduced as \[\begin{aligned} \e&=\lim_{n\to\infty}(1+\frac{1}{n})^n\qquad\text{and as}\\ \e &=1+1+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\frac{1}{120}+\cdots=\sum_{k=0}^{\infty}\frac{1}{k!}\end{aligned}\]
The exponential functionThe exponential function \(f(x)=\e^x\) occurs so often in mathematical work that it is called the exponential function. In textbooks, computer programs and calculators you will also encounter the notation \(\exp(x)\) as synonym of \(\e^x\).
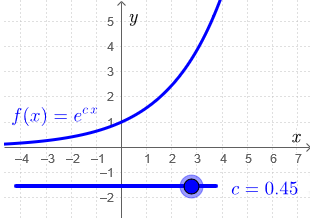
The exponential function defined by \(\e^x\) can be turned into another exponential functions by multiplying the argument \(x\) with a constant \(c\); then we get a function of the following form \[f(x)=\e^{c\cdot x}\] This is an exponential function with base \(\e^c\); Indeed the following equalities are valid: \[\begin{aligned}f(x)&=\e^{c\cdot x}&\\[0.25cm] &=\left(\e^c\right)^x&\\[0.25cm] &=a^x\text{,} & \text{where }a=\e^c\text{.}\end{aligned}\]
Interactive visualisation By moving the slider in the below interactive figure below you can get an idea how the graph of the exponential function \[f(x)=\e^{c\cdot x}\] looks like for various values of \(c\).
Properties The translation of the previously mentioned properties of exponential functions for the exponential function \(f(x)=e^{c\cdot x}\) is as follows:
- \(f(0)=1\).
- \(f(x)>0\) for all \(x\).
- \(f\) is increasing if and only if \(c>0\). The greater the value of \(c\) is, the faster the function increases.
- \(f\) is decreasing if and only if \(c<0\). When \(c\) gets a larger negative value, the function decreases faster.
- The horizontal axis is a horizontal asymptote for each exponential function. For \(c<0\) we have: \(\e^{cx}\to 0\) if \(x\to \infty\). For \(c>0\) we have: \(\e^{c\cdot x}\to 0\) if \(x\to -\infty\).
As illustration of the application of the above properties we present a dynamic example of simplification of powers of \(\e\):
&= \frac{5}{\e^{4\cdot 2\cdot x}}\\ &\phantom{abcxyz} \blue{\text{calculation rules for powers in denominator applied}}\\
&= \frac{5}{\e^{8\cdot x}} \\ &\phantom{abcxyz} \blue{\text{simplification of the denominator}} \\ &=5 \e^{-8 x}\\ &\phantom{abcxyz} \blue{\text{rewritten as }e\text{-power}}\end{aligned}\]