Exponentiële functies en logaritmen: Exponentiële functies
Dé exponentiële functie exp(x)
Het grondtal e
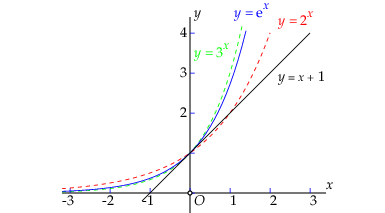
Tussen het grondtal \(a=2\) en het grondtal \(a=3\) zit precies één grondtal, dat we met \(e\) aanduiden, zodanig dat de grafiek van \(f(x)=\e^x\) en de rechte lijn met vergelijking \(y=x+1\) elkaar raken in het punt \((0,1)\), d.w.z. dat de grafieken precies één punt gemeenschappelijk hebben.
De waarde van dit getal is ongeveer \(2.71828\)
De exacte waarde is te beschrijven als \[\begin{aligned} \e&=\lim_{n\to\infty}(1+\frac{1}{n})^n\qquad\text{en als}\\ \e &=1+1+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\frac{1}{120}+\cdots=\sum_{k=0}^{\infty}\frac{1}{k!}\end{aligned}\]
De exponentiële functie De exponentiële functie \(f(x)=\e^x\) komt zo vaak voor, dat deze wel dé exponentiële functie wordt genoemd. In boeken, computerprogramma's en rekenmachines kom je ook wel de notatie \(\exp(x)\) als synoniem voor \(\e^x\) tegen.
Van de exponentiële functie met functievoorschrift \(\e^x\) kunnen we andere exponentiële functies maken door het argument \(x\) met een constante \(c\) te vermenigvuldigen; we krijgen dan een functie van de volgende vorm \[f(x)=e^{c\cdot x}\] Dit is een exponentiële functie met grondtal \(\e^c\); er geldt immers \[\begin{aligned}f(x)&=\e^{c\cdot x}&\\[0.25cm] &=\left(\e^c\right)^x&\\[0.25cm] &=a^x\text{,} & \text{met }a=\e^c\text{.}\end{aligned}\]
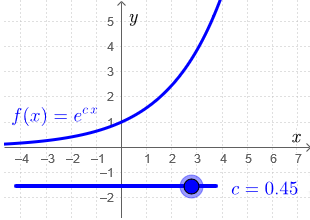
Interactieve visualisatie Door de schuifbalk in onderstaande figuur te bewegen krijg je een idee hoe de grafiek van de exponentiële functie \[f(x)=\e^{c\cdot x}\] er uit ziet voor verschillende waarden van \(c\).
Eigenschappen De vertaling van de eerder genoemde eigenschappen van exponentiële functies voor de exponentiële functie \(f(x)=e^{c\cdot x}\) is als volgt:
- \(f(0)=1\).
- \(f(x)>0\) voor alle \(x\).
- \(f\) is stijgend dan en slechts dan als \(c>0\). Hoe groter \(c\), hoe sneller de functie stijgt.
- \(f\) is dalend dan en slechts dan als \(c<0\). Hoe negatiever \(c\), hoe sneller de functie daalt.
- De horizontale as treedt voor elke exponentiële functie op als horizontale asymptoot.
Voor \(c<0\) geldt: \(\e^{c\cdot x}\to 0\) als \(x\to \infty\).
Voor \(c>0\) geldt: \(\e^{c\cdot x}\to 0\) als \(x\to -\infty\).
Ter illustratie geven we nog een dynamisch voorbeeld van vereenvoudigingen met \(e\)-machten:
&= \frac{3}{\e^{4\cdot 2\cdot x}}\\ &\phantom{abcxyz} \blue{\text{rekenregel voor machten in noemer toegepast}}\\
&= \frac{3}{\e^{8\cdot x}} \\ &\phantom{abcxyz} \blue{\text{de noemer vereenvoudigd}} \\ &=3 \e^{-8 x}\\ &\phantom{abcxyz} \blue{\text{als }\e\text{-macht herschreven}}\end{aligned}\]
