Exponential functions and logarithms: Exponential functions
 Sums of exponential functions
Sums of exponential functions
The diagram below shows the graphs of \(\left(\tfrac{2}{5}\right)^x-\left(\tfrac{1}{5}\right)^x\), \(\left(\tfrac{2}{5}\right)^x\) and \(\left(\tfrac{2}{5}\right)^x\) on the interval \([0,4]\).
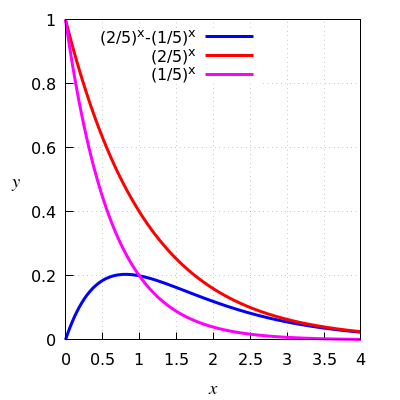
Comparing the graphs we see that the graph of \(\left(\tfrac{2}{5}\right)^x-\left(\tfrac{1}{5}\right)^x\) resembles the graph of \(\left(\tfrac{2}{5}\right)^x\) for large values of \(x\) .
In other words, the \(x\mapsto\left(\tfrac{2}{5}\right)^x-\left(\tfrac{1}{5}\right)^x\) function is very similar to the \(x\mapsto \left(\tfrac{2}{5}\right)^x\) \(x\) for large values of \(x\).
This can also be seen by extracting one of the exponential functions as a factor.
It follows from \(\left(\tfrac{2}{5}\right)^x-\left(\tfrac{1}{5}\right)^x=\left(\tfrac{2}{5}\right)^x\cdot \left(1-\left(\tfrac{1}{2}\right)^x\right)\) that for large values of \(x\) the expression \(1-\left(\tfrac{1}{2}\right)^x\) between brackets is close to \(1\). Then the function looks like \(x\mapsto \left(\tfrac{2}{5}\right)^x\).
In a sum of two or more exponential functions, the function resembles the term with the largest base for large values of \(x\).


