Toepassingen van de exponentiële functie

Exponentiële functies en logaritmen: Exponentiële functies

Toepassingen van de exponentiële functie

Exponentiële functies kom je in wiskundige modellen van veranderingsprocessen keer op keer tegen: uiteraard - nomen est omen - in modellen van exponentiële groei en begrensde exponentiële groei, maar ook bij logistische groei. We zullen dit gebruik van exponentiële functies in wiskundige modellen van groei bestuderen in een later hoofdstuk, nadat we nog meer kennis over deze functies hebben opgedaan. Hier kijken we naar wat andere toepassingen.

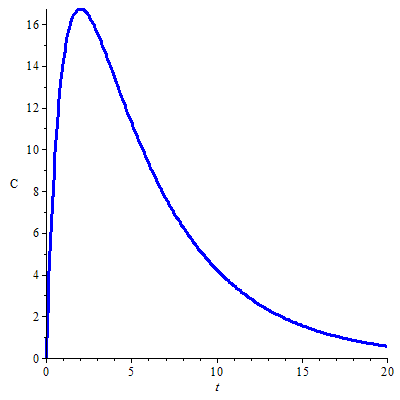
Kwantitatieve farmacokinetiek Een ander toepassingsgebied is kwantitatieve farmacokinetiek. Zo wordt het verloop van de plasmaconcentratie \(C(t)\) van een oraal toegediend farmacon in de loop van de tijd \(t\) vaak wiskundig beschreven door een bi-exponentiële functie, met een term voor absorptie en eliminatie van het farmacon. De bijpassende formule is \[C(t)=\frac{k_a A_0 F }{V_d{(k_a-k)}}\left(\e^{-k\,t}- \e^{-k_a\,t}\right).\] waarbij \(k_a\) de absorptiesnelheidsconstante is, \(k\) de eliminatiesnelheidsconstante, \(A_0\) de toegediende beginhoeveelheid van het farmacon, \(F\) de biologische beschikbaarheid van het farmacon is (d.w.z. de fractie van het toegediende farmacon dat onveranderd in de algemene bloedcirculatie terechtkomt) en \(V_d\) het zogenaamde verdelingsvolume (distributievolume) van het farmacon is. De wiskundige formule is een bi-exponentiële functie omdat het een verschil van twee \(e\)-machten is. Onderstaande figuur toont de grafiek van de plasmaconcentratie van een farmacon berekend met de volgende farmacokinetische parameters: \[\text{orale dosis }A_0=500\,\mathrm{mg},\; k_a=1.0\,\mathrm{h}^{-1},\; k=0.2\,\mathrm{h}^{-1}, \;V_d=10\,\mathrm{L}, F=0.5\,.\]

plasmaconcentratie na orale toediening van een farmacon

Twee voorbeelden van het gebruik van de exponentiële functie in psychobiologie en neurowetenschappen:

Retentie van informatie Hermann Ebbinghaus was een van de eerste psychologen die kwantitatief onderzoek verrichte naar het geheugen. Hij ontdekte dat nieuw aangeleerde dingen eerst volledig gereproduceerd konden worden, maar minder naarmate de tijd verstreek. Hij poneerde een wiskundige formule voor de kans dat informatie onthouden is na een zekere tijd, retentiefunctie \(R(t)\), met behulp van de logaritme. Maar de volgende exponentiële formule voor deze kans is populairder: \[R(t)=(1-R_{\infty})\cdot c\cdot \e^{-r\cdot t}+R_{\infty}\] waarbij de term \(R_{\infty}\) weerspiegelt dat er maar zelden informatie geheel verloren gaat, \(c\) een parameter is met een waarde tussen 0 en 1, en de parameter \(r\) de snelheid bepaalt waarmee informatie verloren gaat. Deze constante hangt van vele factoren af zoals bijvoorbeeld de emotionele betekenis van het geleerde en de wijze waarop de informatie geleerd is.

Vuren van een prikkelbare cel Een Poisson proces is een simpel model voor het vuren van een prikkelbare cel (generatie van een actiepotentiaal). In dit model is de kans \(P(k, \Delta t)\) dat een cel \(k\) keer vuurt in een tijdspanne \(\Delta t\), gegeven door de dichtheid \[P(k, \Delta t)=\frac{\e^{-\lambda\Delta t}(\lambda\Delta t)^k}{k!}\] Stel dat de cel vuurt op tijdstip \(t=0\), dan is de kans \(p(s)\) dat de cel op tijdstip \(t=s\) opnieuw vuurt volgens dit model gelijk aan \[p(s)=\mu\, \e^{-\mu s}\] voor \(\mu=1/\lambda\).

Tot slot twee voorbeelden van een exponentieel verband in de scheikunde, en meer in het bijzonder in chemische reactiekinetiek:

Arrhenius vergelijking De reactiesnelheidsconstante \(k\) voor een chemische reactie hangt vaak exponentieel af de temperatuur \(T\) via de Arrhenius vergelijking \[k=A\cdot \e^{-\frac{E_a}{RT}}\] waarbij \(E_a\) de activeringsenergie is, \(R\) de molaire gasconstante is en \(A\) een constante is.

Reactiekinetiek We bekijken twee opeenvolgende chemische reacties van het type \[\text{A }{\mathop{\longrightarrow}\limits_{}^{k_1}} \text{ B }{\mathop{\longrightarrow}\limits_{}^{k_2}} \text{ C}\] met reactiesnelheidsconstanten \(k_1\) en \(k_2\). Wanneer we er van uit gaan dat zowel \(\text{A }{\mathop{\longrightarrow}\limits_{}^{k_1}} \text{ B}\) als \(\text{B }{\mathop{\longrightarrow}\limits_{}^{k_2}} \text{ C}\) een elementaire reactie is, dan kunnen we het volgende stelsel van differentiaalvergelijkingen opstellen voor de concentraties van A, B en C: \[ \left\{\begin{aligned} \frac{d[\text{A}]}{dt} &= -k_1\, [\text{A}] \\ \\ \frac{d[\text{B}]}{dt} &=k_1\, [\text{A}]-k_2\, [\text{B}]\\ \\ \frac{d[\text{C}]}{dt} &= k_2\, [\text{B}]\end{aligned} \right.\]

De concentraties van elke stof kunnen exact berekend worden, gegeven de beginconcentraties \([\text{A}]_0\), \([\text{B}]_0\), \([\text{C}]_0\). We bekijken het geval dat \([\text{B}]_0=0, [\text{C}]_0=0\): \[ \left\{\begin{aligned} {[\text{A}]} &= [\text{A}]_0\e^{-k_1t} \\ \\ [\text{B}] &= \left\{\begin{array}{lr} [\text{A}]_0k_1\,t\,\e^{-k_1t} & \text{als }k_1=k_2 \\ \\ \dfrac{ [\text{A}]_0\,k_1}{k_2-k_1}\left(\e^{-k_1t}-\e^{-k_2t}\right) & \text{als }k_1\neq k_2 \end{array} \right. \\ \\ [\text{C}] &= [\text{A}]_0-[\text{A}]-[\text{B}]\end{aligned} \right.\]

Voor de liefhebber geven we het bewijs.

We noteren \(x(t)\) resp. \(y(t)\) voor de concentraties \([\text{A}]\) resp. \([\text{B}]\), en we veronderstellen \([\text{A}]_0=a, [\text{B}]_0=0, [\text{C}]_0=0\). De differentiaalvergelijking \[\frac{dx}{dt}=-k_1\, x\] beschrijft exponentieel verval en de oplossing is gelijk aan \[x=a\,\e^{-k_1t}\] Invullen in de differentiaalvergelijking \(\dfrac{dy}{dt}=k_1\,x-k_2\,y\) geeft \[\frac{dy}{dt}=a\,k_1\,\e^{-k_1t}-k_2\,y\] oftewel \[\frac{dy}{dt}+k_2\,y=a\,k_1\,\e^{-k_1t}\] We vermenigvuldigen links en rechts met \(\e^{k_2t}\) en krijgen dan \[\e^{k_2t}\frac{dy}{dt}+k_2\,\e^{k_2t}\,y=a\,k_1\,\e^{(k_2-k_1)t}\] en met behulp van de rekenregels voor differentiëren: \[\frac{d}{dt}\left(\e^{k_2t}\,y\right)=a\,k_1\,\e^{(k_2-k_1)t}\] Dus: \[\e^{k_2t}\,y=a\,k_1\!\int \e^{(k_2-k_1)t}\,dt\] Om de integraal uit te rekenen moeten we twee gevallen onderscheiden.

Als \(k_1=k_2\), dan staat er eigenlijk \[\e^{k_2t}\,y=a\,k_1\!\int 1\,dt\] en krijgen we \[\e^{k_2t}\,y=a\,k_1\,t+C\] voor zekere constante \(C\). Uit \(y(0)=0\) volgt \(C=0\). Dus in dit geval is de oplossing te schrijven als \[y=a\,k_1\,t\,\e^{-k_1t}\]

Als \(k_1\neq k_2\), dan hebben we een exponentiële functie als integrand. De integraal is uit te rekenen en we krijgen: \[\e^{k_2t}\,y=\frac{a\,k_1}{k_2-k_1}\e^{(k_2-k_1)t}+C\] Uit \(y(0)=0\) volgt \[0=\frac{a\,k_1}{k_2-k_1}+C\] oftewel \[C= -\frac{a\,k_1}{k_2-k_1}\] Dus: \[\e^{k_2t}\,y=\frac{a\,k_1}{k_2-k_1}\left(\e^{(k_2-k_1)t}-1\right)\] Herschrijven geeft dan: \[y=\frac{a\,k_1}{k_2-k_1}\left(\e^{-k_1t}-\e^{-k_2t}\right)\]

We geven een simulatie om mee te exploreren. Ga bijvoorbeeld eens na als \(k_1\ll k_2\) de concentratie van stof B laag blijft omdat B snel omgezet wordt in C en dat de kinetiek dus weinig verschilt van die van \(\text{A}{\mathop{\longrightarrow}\limits_{}^{k_1}}\text{C}\). Omgekeerd betekent \(k_2\ll k_1\) dat dan een hoge concentratie van stof B wordt bereikt omdat de tweede reactie \(\text{B }{\mathop{\longrightarrow}\limits_{}^{k_2}}\text{ C}\) traag verloopt en dat stof B dan pas verdwijnt als er nagenoeg geen stof A over is om nog omgezet te worden.

Een concreet voorbeeld van twee opeenvolgende reacties is de thermische ontleding van dimethylether \[\text{CH}_3\text{OCH}_3\longrightarrow \text{CH}_4 + \text{CH}_2\text{O}\longrightarrow \text{CH}_4 + \text{CO} +\text{H}_2\]