Exponential functions and logarithms: Logarithms
The natural logarithm
If \(y\) is a positive real number, then it is clear from the graph of the exponential function that the equation \(\e^x=y\) has exactly one solution. This solution is denoted as \(\ln(y)\), where ln is an abbreviation for natural logarithm.
By definition: \[\ln(y)=x\iff y=\e^x\]
Examples
The equation \(\e^x=2\) has solution \(x=\ln(2)\).
The equation \(\e^x=\tfrac{1}{2}\) has solution \(x=\ln(\tfrac{1}{2})=-\ln(2)\) because then \(\e^{-x}=\frac{1}{\e^x}=2\) and thus \(-x=\ln(2)\).
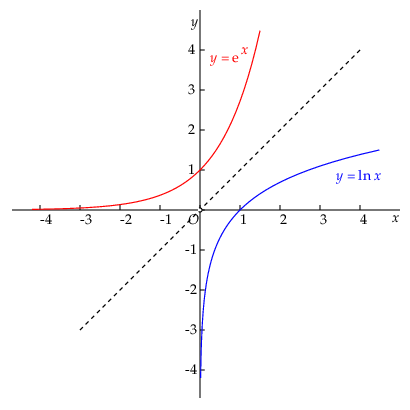
The graph of the natural logarithm
The natural logarithm is thus defined as function \(f(x)=\ln(x)\) for positive real numbers. The natural logarithm graph can be obtained by reflecting the graph of the exponential function in the line \(y=x\) because these functions are each other's inverse, i.e., \[\e^{\ln(x)}=\ln(\e^x)=x\] for positive values of \(x\).
The vertical axis is the vertical asymptote of the natural logartithm.
\ln(x\cdot y) &= \ln(x)+\ln(y)\\ \\
\ln\left(\frac{x}{y}\right) &= \ln(x)-\ln(y) \\ \\
\ln(x^r) &= r\cdot\ln(x) \\ \\
\ln(1) &= 0
\end{aligned}\]
As an example of a proof of a calculation rule, we consider the first one.
We know from the calculation rules for exponential functions all that \[\e^{\ln(x)}\cdot \e^{\ln(y)} = \e^{\ln(x)+\ln(y)}\] On the other hand, by definition, to the left hand side which \[\e^{\ln(x)}\cdot \e^{\ln(y)}= x\cdot y = \e^{\ln(x\cdot y)}\] The combination of these two equations yields: \[\e^{\ln(x\cdot y)}= \e^{\ln(x)+\ln(y)}\] Equating the exponents then gives the calculation rule \[\ln(x\cdot y) = \ln(x)+\ln(y)\]
To illustrate the calculation rules, we give examples of consistent application of the calculation rules in order to achieve a simplification of a mathematical experession. The calculation rules are also applied when solving an equation in which the natural logarithm is present.
\[\begin{aligned} \ln(\e^4) &= 4\cdot\ln(e)&\blue{\text{calculation rule }\ln(x^r)=r\cdot \ln(x)} \\[0.25cm]&=4\cdot 1&\blue{\text{by definition}} \\[0.25cm]&=4&\blue{\text{simplification}} \end{aligned}\] The result can also be found by application of calculating rules in a different order.
