De natuurlijke logaritme

Exponentiële functies en logaritmen: Logaritmen

De natuurlijke logaritme

Als $y$ een positief reëel getal is, dan volgt uit de grafiek van de exponentiële functie dat de vergelijking $\e^x=y$ precies één oplossing heeft. Deze oplossing noteren we als $\ln(y)$ , waarbij ln een afkorting is voor natuurlijke logaritme.

Per definitie geldt dus: $\ln(y)=x\iff y=\e^x$

Voorbeelden

De vergelijking $\e^x=2$ heeft als oplossing $x=\ln(2)$ .

De vergelijking $\e^x=\tfrac{1}{2}$ heeft als oplossing $x=\ln(\tfrac{1}{2})=-\ln(2)$ omdat dan $\e^{-x}=\frac{1}{\e^x}=2$ en dus $-x=\ln(2)$ .

De grafiek van de natuurlijke logaritme

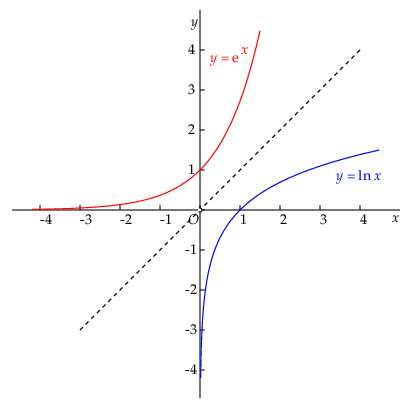
De natuurlijke logaritme is hiermee gedefinieerd als functie $f(x)=\ln(x)$ voor positieve reële getallen. De grafiek van de natuurlijke logaritme is kun je verkrijgen door de grafiek van de exponentiële functie in de lijn $y=x$ te spiegelen want deze functies zijn elkaars inverse, d.w.z. $\e^{\ln(x)}=\ln(\e^x)=x$ voor positieve waarden van $x$ .

De verticale as is de asymptoot van de natuurlijke logaritme.

grafiek van de natuurlijke logartime

Uit de eigenschappen van de exponentiële functie kunnen eigenschappen van de natuurlijke logaritme worden afgeleid. Voor alle positieve reële getallen $x$ en $y$ , en voor elk rationaal getal $r$ geldt $\begin{aligned} \ln(x\cdot y) &= \ln(x)+\ln(y)\\ \\ \ln\left(\frac{x}{y}\right) &= \ln(x)-\ln(y) \\ \\ \ln(x^r) &= r\cdot\ln(x) \\ \\ \ln(1) &= 0 \end{aligned}$

Als voorbeeld van een bewijs van een rekenregel bekijken we de eerste.

We weten op basis van rekenregels voor exponentiële functies al dat $\e^{\ln(x)}\cdot \e^{\ln(y)} = \e^{\ln(x)+\ln(y)}$ Anderzijds geldt per definitie voor het linkerlid dat $\e^{\ln(x)}\cdot \e^{\ln(y)}= x\cdot y = \e^{\ln(x\cdot y)}$ De combinatie van deze twee gelijkheden levert op: $\e^{\ln(x\cdot y)}= \e^{\ln(x)+\ln(y)}$ Gelijkstelling van de exponenten geeft dan de rekenregel $\ln(x\cdot y) = \ln(x)+\ln(y)$

Ter illustratie van de rekenregels geven we voorbeelden van consequent toepassen van de rekenregels om een vereenvoudiging van een wiskundige uitdrukking te bewerkstelligen. Deze rekenregels worden ook toegepast bij het oplossen van een vergelijking waarin de natuurlijke logaritme aanwezig is.

Vereenvoudig zo veel mogelijk: $\quad\ln\left(\frac{1}{\e^4}\right)$

$-4$

$\begin{aligned} \ln\left(\frac{1}{\e^4}\right) &= \ln\left(\e^{-4}\right)&\blue{\text{rekenregel voor machten}} \\[0.25cm]&=-4\cdot\ln(\e)&\blue{\text{rekenregel } \ln(x^r)=r\cdot \ln(x)} \\[0.25cm]&=-4\cdot 1&\blue{\text{per definitie}} \\[0.25cm]&=-4&\blue{\text{vereenvoudiging}} \end{aligned}$ Het resultaat kan ook via toepassing van rekenregels in andere volgorde bereikt worden.

Nieuw voorbeeld