We gaan verscheidene kwadratuurformules bestuderen voor benadering van de integraal $\displaystyle \int_a^b f(x)\,\dd x$ van een functie $f(x)$ over een interval $[a,b]$. We verdelen hierbij steeds het interval $[a,b]$ in $n$ stukjes door in dat interval vaste punten $x_0, x_1, x_2,\ldots, x_n$ aan te wijzen met

$$a = x_0 < x_1 < x_2 < \cdots < x_n = b\tiny.$$ Zo'n verzameling heet wel een verdeling $V$ van $[a,b]$. Vervolgens kiezen we in elk van de deelintervallen $[x_{k-1},x_k]$ een strooipunt $s_k$. Dus $x_{k-1}\le s_k\le x_k$ voor $k = 1, 2, \ldots n$. De lengte van elk van de deelintervallen $[x_{k-1},x_k]$ geven we aan met ${\vartriangle}_k=x_k-x_{k-1}$ en het maximum van de lengtes van de deelintervallen noemen we de maaswijdte. De uitdrukking $$R(V; s_1, \ldots, s_n)=\sum_{k=1}^nf(s_k)\cdot {\vartriangle}_k$$ heet een Riemannsom behorend bij de functie $f$. Merk op: bij een gegeven verdeling $V$ van $[a, b]$ horen veel verschillende Riemannsommen: bij elke keuze van strooipunten krijg je er telkens een. Hieronder zijn bij een zekere verdeling $V$ van $[a, b]$, waarbij dat interval in drie stukjes verdeeld wordt, drie Riemannsommen gegeven: links een 'willekeurige', daarnaast de grootst mogelijke Riemannsom die je bij $V$ kunt maken (bovensom), en rechts de kleinst mogelijke (ondersom).

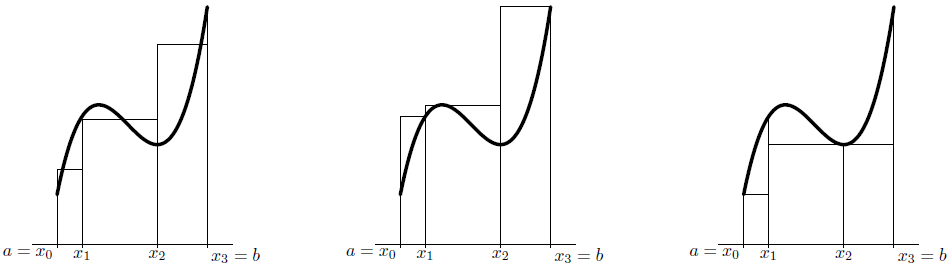
Zo'n Riemannsom is dus de som van de oppervlaktes van rechthoekjes. Deze rechthoekjes samen vormen een benadering van de oppervlakte onder een grafiek die we willen berekenen. De gevraagde oppervlakte is in zekere zin een limiet van zulke Riemannsommen. Een visualisatie van de Riemannsommen is hieronder geplaats om mee te spelen zodat je een beter beeld van de verschillende situaties (bovensom, ondersom. kunt krijgen.

Een Riemannsom is een speciaal geval van een kwadratuurformule, die geschreven kan worden als

$$K(V; s_1, \ldots, s_n)=\sum_{k=1}^nf(s_k)\cdot w_k$$ voor zekere gewichten $w_1,w_2,\ldots,w_n$. Vaak zullen de strooipunten samenvallen met punten van de verdeling $V$ en zal elk gewicht bestaan uit het product van ${\vartriangle}_k$ en een som van functiewaarden in strooipunten en punten van de verdeling $V$ in de omgeving van strooipunt $s_k$. Als de strooipunten op gelijke onderlinge afstand, d.w.z. equidistant, gekozen zijn spreken we van een Newton-Cotes kwadratuurformule; als de strooipunten niet equidistant gekozen zijn dan spreken we van een Gauss kwadratuurformule. De laatstgenoemde categorie van kwadratuurformules bevat de beste integratiemethoden, maar deze zullen we niet bespreken.

In dit hoofdstuk zullen een aantal bekende Riemannsommen en kwadratuurformules de revue passeren en de taak is steeds om de besproken methode in een programmeertaal te implementeren en te gebruiken in de volgende twee gevallen

• $\displaystyle \int_0^1\frac{4}{x^2+1}\,\dd x=\pi$
  
  
• $\displaystyle \int_0^{\pi}\sin(x)\,\dd x=2$
  
  

Ook zullen we aandacht besteden aan de afbreekfouten van de verschillende benaderingen.