The trapezoidal rule, also known as the trapezoid rule or trapezium rule, can be derived by approximating \(f(x)\) on the interval \([a,b]\) with \(n\) segments connecting successive points of the partition consisting of \(n+1\) equidistant points on the interval \(h=\frac{b-a}{n}\). The figure below visualises this.

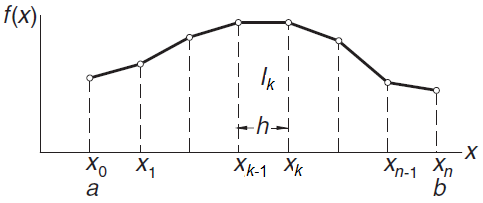
So we start by dividing the interval \([a,b]\) into \(n\) equal pieces with mesh size \(h\). The points of this partition are \(x_k=a+k h\) with \(k=0,1,\ldots n\). Let's look at the subinterval \([x_{k-1},x_k]\). We approximate the integral \[\int_{x_{k-1}}^{x_{k}}f(x)\,\dd x\] with the area \(I_k\) of the trapezoid with vertices \(\bigl(x_{k-1},0\bigr)\), \(\bigl(x_{k-1},f(x_{k-1})\bigr)\), \(\bigl(x_{k},f(x_{k})\bigr)\) and \(\bigl(x_{k},0\bigr)\). This can easily be to computed geometrically: \[I_k=\frac{h}{2}\bigl(f(x_{k-1})+f(x_{k})\bigr)\] Summing over all subintervals we get \[\begin{aligned}I&=\sum_{k=1}^nI_k=\sum_{k=1}^n \frac{h}{2}\bigl(f(x_{k-1})+f(x_k)\bigr) \\ \\ &= \frac{h}{2}f(x_0)+h\left(\sum_{k=1}^{n-1} f(x_k)\right)+\frac{h}{2}f(x_n) \\ \\ &= \frac{h}{2}f(a)+h\left(\sum_{k=1}^{n-1} f(a+kh)\right)+\frac{h}{2}f(b)\end{aligned}\] We have found the following result.

These sums are used to approximate the area under the curve. Below is a visualisation of the trapezoidal rule for you to play with, so that you can get a better idea of the trapezoidal rule.

Programming task

Write a function TrapezoidalRule(f,a,b,n) that implements the Trapezoidal rule.

Apply your function with \(n=100\) in the following two cases:

• \(\displaystyle \int_0^1\frac{4}{x^2+1}\,\dd x=\pi\)
  
  
• \(\displaystyle \int_0^{\pi}\sin(x)\,\dd x=2\)