De trapeziumregel kan afgeleid worden door de functie \(f(x)\) op het interval \([a,b]\) te benaderen met \(n\) lijnstukjes die opeenvolgende punten van de verdeling met elkaar verbinden, voor een verdeling van \(n+1\) equidistante punten op het interval met maaswijdte \(h=\frac{b-a}{n}\). Onderstaande figuur visualiseert dit.

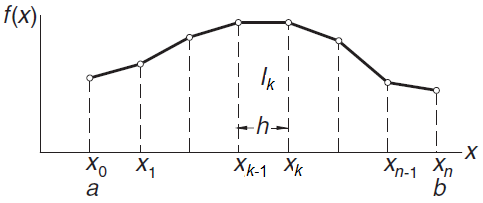
We beginnen dus met het verdelen van het interval \([a,b]\) in \(n\) gelijke stukken met maaswijdte \(h\). De punten van de verdeling zijn \(x_k=a+k h\) met \(k=0,1,\ldots n\). We bekijken het deelinterval \([x_{k-1},x_k]\). We benaderen de integraal \[\int_{x_{k-1}}^{x_{k}}f(x)\,\dd x\] met de oppervlakte \(I_k\) van het trapezium met hoekpunten \(\bigl(x_{k-1},0\bigr)\), \(\bigl(x_{k-1},f(x_{k-1})\bigr)\), \(\bigl(x_{k},f(x_{k})\bigr)\) en \(\bigl(x_{k},0\bigr)\). Deze is gemakkelijk meetkundig uit de rekenen: \[I_k=\frac{h}{2}\bigl(f(x_{k-1})+f(x_{k})\bigr)\] Sommeren we over alle deelintervallen dan krijgen we \[\begin{aligned}I&=\sum_{k=1}^nI_k=\sum_{k=1}^n \frac{h}{2}\bigl(f(x_{k-1})+f(x_k)\bigr) \\ \\ &= \frac{h}{2}f(x_0)+h\left(\sum_{k=1}^{n-1} f(x_k)\right)+\frac{h}{2}f(x_n) \\ \\ &= \frac{h}{2}f(a)+h\left(\sum_{k=1}^{n-1} f(a+kh)\right)+\frac{h}{2}f(b)\end{aligned}\] We hebben hiermee het volgende resultaat gevonden.

Deze sommen worden gebruikt om de oppervlakte van het gebied onder \(f\) te benaderen. Een visualisatie van de trapeziumregel is hieronder geplaatst om mee te spelen opdat je een beter beeld van de trapeziumregel kunt krijgen.

Programmeeropdracht

Schrijf een functie Trapeziumregel(f,a,b,n) die de trapeziumregel implementeert.

Pas jouw functie toe met \(n=100\) in de volgende twee gevallen:

• \(\displaystyle \int_0^1\frac{4}{x^2+1}\,\dd x=\pi\)
  
  
• \(\displaystyle \int_0^{\pi}\sin(x)\,\dd x=2\)