Simpson's rule can be derived by approximating the function \(f(x)\) on the interval \([a,b]\) by connecting three consecutive points of the partition with a parabola, then treating the next set of three points in the partition in the same way, and continuing until you reach the end of the interval \([a,b]\), for a partition of \(n+1\) equidistant points on the interval with mesh size \(h=\frac{b-a}{n}\). So we assume that \(n\) is even, say \(n=2m\). The figure below visualizes the situation for \(n=2\).

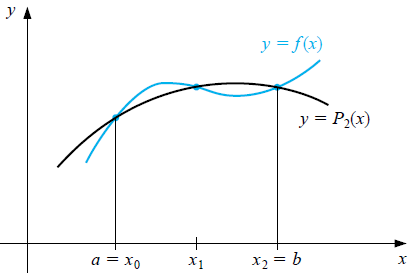
The parabola \(P_2(x)\) can be found via Lagrange interpolation and the formula is \[\begin{aligned}P_2(x) &= \;\;\;\,\,\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}f(x_0)\\ \\ &\phantom{=}{}+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}f(x_1) \\ \\ &\phantom{=} {}+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}f(x_2)\end{aligned}\] with \(x_0=a, x_1=a+h, x_2=a+2h\). In other words: \[\begin{aligned}P_2(x)&=\frac{(x-a-h)(x-a-2h)}{2h^2}f(x_0)\\ \\ &\phantom{=}-\frac{(x-a)(x-a-2h)}{h^2}f(x_1)\\ \\ &\phantom{=}+\frac{(x-a)(x-a-h)}{2h^2}f(x_2)\end{aligned}\] Then we get with the substitution rule for \(y=\frac{x-a}{h}\) that \[\begin{aligned}\int_a^bP_2(x)\,\dd x &= f(x_0)\int_0^2\frac{(y-1)(y-2)}{2}dy-f(x_1)\int_0^2y(y-2)\,dy\\ &\phantom{=}+f(x_2)\int_0^2y(y-1)\,dy\\ \\ &= \frac{h}{3}\bigl(f(x_0)+4f(x_1)+f(x_2)\bigr)\end{aligned}\]

We can now look at a refined partition. The points of the partition are \(x_k=a+k h\) with \(k=0,1,\ldots 2m\) and we can divide them into groups of 3: \(\{x_{2k-2},x_{2k-1},x_{2k}\}\) for \(k=1,\ldots m\). At each sub-interval \([x_{2k-2},x_{2k-1}, x_{2k}]\) we approximate the integral \[\int_{x_{2k-2}}^{x_{2k}}f(x)\,\dd x\] with the area \(I_k\) under the parabola through the points \(\bigl((x_{2k-2},f(x_{2k-2}\bigr))\), \(\bigl(x_{2k-1},f(x_{2k-1})\bigr)\) and \(\bigl(x_{2k},f(x_{2k})\bigr)\). See the figure below to get an impression of how this works.

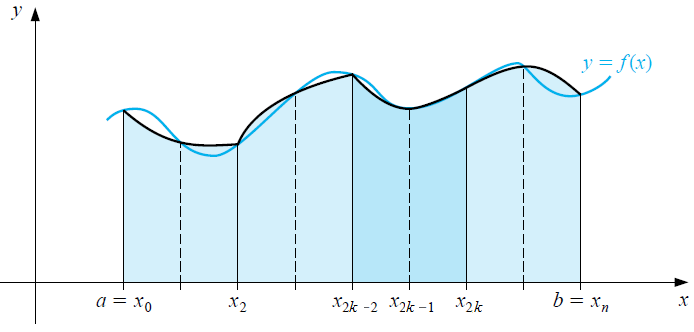
Above we have already derived the approximation formula for each sub-interval: \[I_k=\frac{h}{3}\bigl(f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})\bigr)\] Summing over all sub-intervals we get \[\begin{aligned}I&=\sum_{k=1}^mI_k=\sum_{k=1}^m \frac{h}{3}\bigl(f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})\bigr) \\ \\ &= \frac{h}{3}\bigl(f(a)+f(b) +2\sum_{k=1}^{m-1} f(a+2kh)+4\sum_{k=1}^{m} f(a+(2k-1)h)\bigr)\end{aligned}\] We have thus found the following result.

In case we allow points halfway through a sub-interval, we can also rewrite Simpson's rule, as \[\int_a^bf(x)\,\dd x \approx \frac{h}{6}\Bigl(f(a)+f(b)+2\sum_{k=1}^{n-1} f(a+kh)+4\sum_{k=1}^{n} f\bigl(a+(k-\tfrac{1}{2})h\bigr)\Bigr)\] Then you can better see that

Simpson's formula \({}=\tfrac{1}{3}\cdot{}\) trapezoid rule \({}+\tfrac{2}{3}\cdot{}\) midpoint-Riemann sum

We already know that the truncation error of the midpoint Riemann sum and the trunctation error of the trapezoidal rule are quadratic in mesh size \(h\); so Simpson's rule is at least quadratic in \(h\), but in reality Simpson's rule is an even better approximation.

Programming task

Write a function SimpsonRule(f,a,b,n) that implements Simpson's rule.

Apply your function with \(n=100\) in the following two cases:

• \(\displaystyle \int_0^1\frac{4}{x^2+1}\,\dd x=\pi\)
  
  
• \(\displaystyle \int_0^{\pi}\sin(x)\,\dd x=2\)