Simpson's regel kan afgeleid worden door de functie \(f(x)\) op het interval \([a,b]\) te benaderen door drie opeenvolgende punten van de verdeling met elkaar verbinden d.m.v. een parabool, dan de volgende verzameling van drie punten in de verdeling net zo te behandelen, en doorgaan tot je het einde van het interval \([a,b]\) bereikt hebt, voor een verdeling van \(n+1\) equidistante punten op het interval met maaswijdte \(h=\frac{b-a}{n}\). We veronderstellen dus dat \(n\) even is, zeg \(n=2m\). Onderstaande figuur visualiseert de situatie voor \(n=2\).

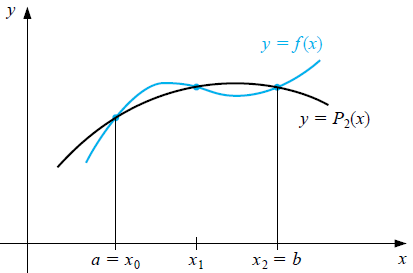
De parabool \(P_2(x)\) kunnen we via Lagrange-interpolatie vinden en de formule is \[\begin{aligned}P_2(x) &= \;\;\;\,\,\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}f(x_0)\\ \\ &\phantom{=}{}+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}f(x_1) \\ \\ &\phantom{=} {}+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}f(x_2)\end{aligned}\] met \(x_0=a, x_1=a+h, x_2=a+2h\). Met andere woorden: \[\begin{aligned}P_2(x)&=\frac{(x-a-h)(x-a-2h)}{2h^2}f(x_0)\\ \\ &\phantom{=}-\frac{(x-a)(x-a-2h)}{h^2}f(x_1)\\ \\ &\phantom{=}+\frac{(x-a)(x-a-h)}{2h^2}f(x_2)\end{aligned}\] Dan geldt met de substitutieregel voor \(y=\frac{x-a}{h}\) dat \[\begin{aligned}\int_a^bP_2(x)\,\dd x &= f(x_0)\int_0^2\frac{(y-1)(y-2)}{2}dy-f(x_1)\int_0^2y(y-2)\,dy\\ &\phantom{=}+f(x_2)\int_0^2y(y-1)\,dy\\ \\ &= \frac{h}{3}\bigl(f(x_0)+4f(x_1)+f(x_2)\bigr)\end{aligned}\]

We kunnen nu een fijnere verdeling bekijken. De punten van de verdeling zijn \(x_k=a+k h\) met \(k=0,1,\ldots 2m\) en kunnen we in groepjes van 3 onderverdelen: \(\{x_{2k-2},x_{2k-1},x_{2k}\}\) voor \(k=1,\ldots m\). Op elk deelinterval \([x_{2k-2},x_{2k-1}, x_{2k}]\) benaderen we de integraal \[\int_{x_{2k-2}}^{x_{2k}}f(x)\,\dd x\] met de oppervlakte \(I_k\) onder de parabool door de punten \(\bigl((x_{2k-2},f(x_{2k-2}\bigr))\), \(\bigl(x_{2k-1},f(x_{2k-1})\bigr)\) en \(\bigl(x_{2k},f(x_{2k})\bigr)\). Zie onderstaande figuur om een indruk te hebben hoe dat gaat.

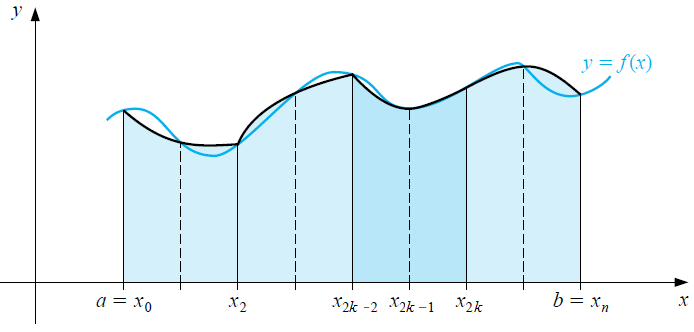
De benaderingsformule op elk deelinterval hebben we hierboven al afgeleid: \[I_k=\frac{h}{3}\bigl(f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})\bigr)\] Sommeren we over alle deelintervallen dan krijgen we \[\begin{aligned}I&=\sum_{k=1}^mI_k=\sum_{k=1}^m \frac{h}{3}\bigl(f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})\bigr) \\ \\ &= \frac{h}{3}\bigl(f(a)+f(b) +2\sum_{k=1}^{m-1} f(a+2kh)+4\sum_{k=1}^{m} f(a+(2k-1)h)\bigr)\end{aligned}\] We hebben hiermee het volgende resultaat gevonden.

In het geval we punten halverwege een deelinterval toestaan, kunnen we Simpson's regel ook herschrijven, als \[\int_a^bf(x)\,\dd x \approx \frac{h}{6}\Bigl(f(a)+f(b)+2\sum_{k=1}^{n-1} f(a+kh)+4\sum_{k=1}^{n} f\bigl(a+(k-\tfrac{1}{2})h\bigr)\Bigr)\] Dan kun je beter zien dat

Simpson's formule \({}=\tfrac{1}{3}\cdot{}\)trapeziumregel\({}+\tfrac{2}{3}\cdot{}\)middelpunt-Riemannsom

We weten al dat de afbreekfout van de middelpunt-Riemannsom en trapeziumregel kwadratisch in de maaswijdte \(h\) zijn; dus is Simpson's regel minstens kwadratisch in \(h\), maar in werkelijkheid is Simpson's regel een nog veel betere benadering.

Programmeeropdracht

Schrijf een functie Simpsonregel(f,a,b,n) die de Simpson's regel implementeert.

Pas jouw functie toe met \(n=100\) in de volgende twee gevallen:

• \(\displaystyle \int_0^1\frac{4}{x^2+1}\,\dd x=\pi\)
  
  
• \(\displaystyle \int_0^{\pi}\sin(x)\,\dd x=2\)