In wetenschappelijk rekenen wordt ook vaak een Monte Carlo methode gebruikt. Een Monte Carlo methode is een aanpak om een wiskundig probleem op te lossen door een geschikt aantal willekeurig getrokken punten de genereren en te bepalen wat de fractie van de punten is met een bepaalde eigenschap.

Monte Carlo integratie van een functie \(f(x)\) op een interval is gebaseerd op de berekening van de oppervlakte van een gebied onder de kromme—dit gebied geven we hier aan met \(O_f\) en de oppervlakte met \(\mathrm{opp}(O_f)\)— via de volgende aanpak. Kies een gebied \(O\) dat \(O_f\) omvat en waarvan je de oppervlakte \(\mathrm{opp}(O)\) kent of gemakkelijk uit kunt rekenen; meestal kiest men voor \(O\) een rechthoek, maar dit hoeft niet per se. Genereer nu volstrekt willekeurig een aantal punten binnen het gebied \(O\) en bepaal hoeveel punten binnen het deelgebied \(O_f\) liggen en hoeveel niet. De oppervlakte van \(O_f\) kun je dan inschatten als de oppervlakte van het geid \(O\) maal de fractie van het aantal punten dat bij de steekproef binnen \(O_f\) valt.

Als het zoekgebied \(O\) eenmaal gekozen is komt de Monte Carlo integratiemethode op het volgende neer (zie onderstaande figuur):

• Neem een voldoende grote steekproef van punten in het zoekgebied \(O\).
• Bepaal de fractie \(p\) van punten die binnen het deelgebied \(O_f\) liggen.
• \(\mathrm{opp}(O_f)\approx p\times \mathrm{opp}(O)\).

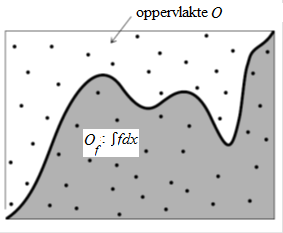
Bovenstaande figuur suggereert dat men het gebied \(O\) zo nauw mogelijk om het gebied \(O_f\) kiest. maar dit is niet noodzakelijk. De stappen uit de Monte Carlo integratiemethode om \(\displaystyle \int_a^bf(x)\,\dd x\) op het interval \([a,b]\) voor een niet-negatieve functie \(f\) te benaderen kun ook de volgende zijn:

Stap 1. Kies een rechthoekig zoekgebied \(O\) van punten \((x,y\) waarvoor geldt dat \(x_{\min}\le x\le x_{\max}\) en \(y_{\min}\le y\le y_{\max}\) bij geschikt gekozen \(x_{\min}, x_{\max}, y_{\min}, y_{\max}\) zodanig dat \[a\le x_{\min},\quad x_{\max}\le b,\quad y_{\min}\le f(x) \le y_{\max}\;\;\text{voor alle }x\text{ in }[a,b]\text.\] Het basisidee is om uit het zoekgebied dat je krijgt door uit het gebied onder de grafiek van \(f\) zoveel mogelijk stukken weg te laten waarvan je de oppervlakte al kent.

Stap 2. Neem een voldoende grote steekproef van punten \((x,y)\) in het zoekgebied \(O\). Dit kun je doen door een uniforme trekking van waarden \(x\) uit \([x_{\min},x_{\max}]\) en een even grote uniforme trekking van waarden \(y\) uit \([y_{\min},y_{\max}]\).

Stap 3. Noem een punt \((x,y)\) in \(O\) 'goed' als \(y\le f(x)\). Merk op dat deze definitie alleen toepasbaar is voor een positieve functie; bij een negatieve functie is de definitie van goedheid juist tegenovergesteld. Het algemene geval is ook te behandelen, eventueel door het interval waarover geïntegreerd wordt op te splitsen in stukken waar de functie alleen positief of alleen negatief is. Een punt noemen we 'fout' als het niet goed is. Tel in je steekproef het aantal goede punten (\(N_\mathrm{goed}\)) en het aantal foute punten (\(N_\mathrm{fout}\)).

Stap 4. De oppervlakte onder de grafiek \(f\) binnen het zoekgebied \(O\) is nu gegeven door \[\mathrm{opp}(O_f)=\frac{N_\mathrm{goed}}{N_\mathrm{goed}+N_\mathrm{fout}}(x_{\max}-x_{\min})(y_{\max}-y_{\min})\]

Stap 5. Bepaal nu de numerieke benadering van \(\displaystyle \int_a^bf(x)\,\dd x\) op het interval \([a,b]\) door bij het resultaat van de vorige stap nog de oppervlakten van de ontbrekende stukken op te tellen.

Python opdracht

Schrijf een eigen functie MonteCarloIntegraal(f, a, b, steekproefGrootte=1000) dat bovenstaande stappenplan implemeneert.

Pas jouw functie toe met een steekproefgrootte van \(100\,000\) punten in de volgende twee gevallen:

• \(\displaystyle \int_0^1\frac{4}{x^2+1}\,\dd x=\pi\)
  
  
• \(\displaystyle \int_0^{\pi}\sin(x)\,\dd x=2\)