Numeriek differentiëren: Tijdreeksen
 Terminologie en voorbeelden
Terminologie en voorbeelden
Terminologie Een tijdreeks of signaal is gedefinieerd als een grootheid die meestal van tijd afhangt, maar in feite van elke andere onafhankelijke variabele of variabelen af mag hangen. Een tijdreeks heet continu, oftewel een signaal heet analoog, als er waarnemingen voortdurend in tijd plaats vinden, zelf als de waargenomen grootheid alleen een eindig aantal waarden aan kan nemen (bijvoorbeeld een aan/uit proces). Een tijdreeks heet discreet wanneer alleen op specifieke tijdstippen, meestal met gelijke tussenpozen, waarnemingen gedaan worden. Dit kan bijvoorbeeld de reeks waterstanden in Vlissingen gemeten op vaste tijdstippen per dag zijn. Ook kunnen het gegevens betreffen die met een sensor gemeten zijn in de loop van de tijd, meestal met vaste meetfrequentie ('sampling rate'). Een tijdreeks kan ook berekende grootheden betreffen; als voorbeeld kun je denken aan de gemiddelde dagtemperatuur in de Bilt die door het KNMI in de loop van tijd vastgesteld wordt. Een tijdsreeks of signaal heet deterministisch als toekomstige waarden voorspelt kunnen worden op basis van de tot dan tot bekende waarnemingen; als dat niet kan spreken we van een stochastische tijdreeks.
Notatie Kenmerkend voor een discrete tijdreeks is dat het gaat om een reeks getallen \[y_0, y_1, y_2, y_3, \ldots \] die geïndexeerd worden met natuurlijke getallen \(0, 1, 2, \ldots\) Elke waarde \(y_k\) staat voor een meting van een grootheid \(y\) op een tijdstip \(t_k\) of voor een accumulatie van een grootheid over tijdsintervallen (bijvoorbeeld, het aantal passanten per uur). Met andere woorden, de tijdreeks bevat waarnemingen van een onbekende functie \(y\) van tijd \(t\). De functie zelf is meestal onbekend; we kennen alleen (benaderingen van) functiewaarden op verschillende tijdstippen. Een tijdreeks kan een eindig of oneindig aantal gegevens betreffen.
Omdat het voor de wiskundige theorievorming handiger is, worden tijdreeksen vaak geïndexeerd met gehele getallen Je kunt bovenstaande tijdreeks aan de linkerkant aanvullen met nullen en dan valt deze tijdreeks ook onder de beschrijving \(y_n\) met \(n\) geheel: \[\ldots, y_{-3}, y_{-2}, y_{-1}, y_0, y_1, y_2, y_3, \ldots \] Een tijdreeks kan meer-dimensionaal zijn: in een 2-dimensionale tijdreeks gebruik je twee indices om de functiewaarden te labelen.
Voorbeeld 1
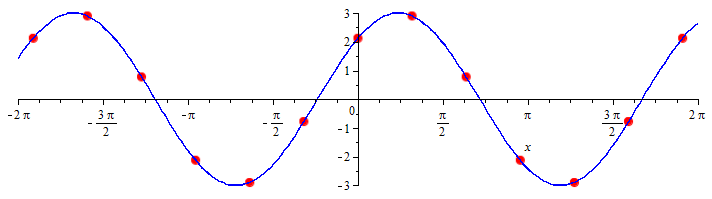
De sinusoïde met amplitude \(A\), frequentie \(f\) en fasehoek \(\varphi\), dat wil zeggen de functie gedefinieerd door \[y(t)=A\cdot \sin(2\pi\cdot f\cdot t+\varphi)\] is een continue tijdreeks. De tijdreeks die je hieruit krijgt voor \(t=\ldots -2,-1,0,1,2,\ldots\),dat wil zeggen \[y_n =A\cdot \sin(2\pi\cdot f\cdot n+\varphi)\] is een voorbeeld van een discrete tijdreeks. Ze zijn samen in onderstaande figuur getekend voor \(A=3, f=\tfrac{1}{6}, \varphi=\tfrac{1}{4}\pi\).
Voorbeeld 2
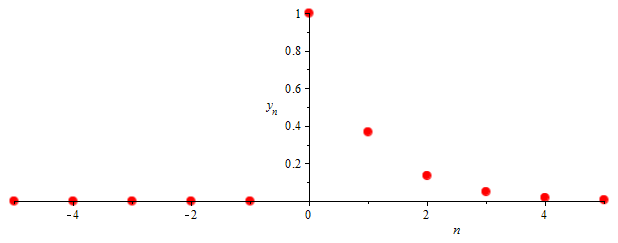
De reeks gedefinieerd door \[y_n=\left\{\begin{array}{ll} e^{-n} & \mathrm{als\;}n=0,1,2,\ldots,\\ 0 & \mathrm{als\;}n=-1,-2,\ldots\end{array}\right.\] is een discrete tijdreeks met onderstaande puntgrafiek.
Voorbeeld 3
Het volgende digitale beeld met afmeting \(128\times 128\) en 8-bits grijswaarden (tussen 0 en 255) is een 2-dimensionaal discreet signaal.

Het gaat hier om 128 horizontale rijtjes van 128 pixels die elk een eigen grijswaarde uit \(\{0,1,2,\ldots, 255\}\) hebben. Er zijn nu twee indices nodig: in de \(i\)-de rij en \(j\)-de kolom (tellend als bij matrices) is de functiewaarde \(g_{i,j}\) een getal uit \(\{0,1,2,\ldots, 255\}\).
Met tijdreeksen wordt gewerkt in elk gebied waarin alleen discrete waarden beschikbaar zijn, zoals bijvoorbeeld in signaalverwerking, patroonherkenning, beeldbewerking, en regeltechniek.
Ook voor een functie beschreven in de vorm van een tijdreeks wil je afgeleiden kunnen uitrekenen, de oppervlakte onder de kromme kunnen berekenen, enzovoort. Het vakgebied dat zich bezig houdt met het analyseren van tijdreeksen heet tijdreeksanalyse en ook wel signaalanalyse. Het vinden van een trend in meetgegevens is een voorbeeld van een dergelijke analyse, die je in staat stelt om voorspellingen te doen. Maar ook het verwerken van storingen in metingen ('data smoothing') hoort tot deze discipline. Een belangrijk onderdeel van de verwerking van periodieke signalen is fourieranalyse en meer in het algemeen spectraalanalyse; in deze cursus gaan we hier niet op in, maar je komt het ongetwijfeld in je studie tegen.
In dit hoofdstuk beschrijven we vooral hoe afgeleiden van tijdreeksen uitgerekend kunnen worden en welke methoden het meest geschikt zijn voor dit numeriek differentiëren.
Veronderstelling Voor het gemak zullen we hierbij steeds veronderstellen dat de gegevens in een tijdreeks met vaste tijdstappen waargenomen of bekend zijn, dat wil zeggen dat de tijdstap \(t_{k+1}-t_{k}\) constant is voor alle indices \(k\).


