Numeriek differentiëren: Tijdreeksen
 Filters
Filters
Een filter is in wezen niets anders dan een omzetting van de ene tijdreeks in een andere. Meestal gebruik je ze om onderdelen samengestelde signalen op basis van een of ander criterium wel of niet door te laten. Een geluidsfilter kan bijvoorbeeld gebruikt om achtergrondgeluiden te verminderen. Een andere toepassing is om ruis in meetgegevens weg te filteren, in het Engels vaak aangeduid met 'data smoothing'.
Omdat numerieke afgeleiden van meetgegevens erg gevoelig zijn voor zelfs kleine meetfouten, bekijken we als intermezzo hoe je dergelijke ruis kunt wegfilteren. We bekijken steeds een tijdreeks \(x_n\) en construeren daaruit een nieuwe tijdreeks \(y_n\). Randeffecten negeren we voor het gemak.
Voortschrijdend gemiddelde Een voortschrijdend gemiddelde is het gemiddelde van een vast aantal opeenvolgende elementen in een tijdreeks. Meestal neemt met \(2q+1\) opeenvolgende punten, voor zeker natuurlijk getal \(q\) (de filterbreedte, ook wel data venster genoemd), rondom een punt in de tijdreeks \(x_n\) om een nieuw element met dezelfde index te creëren, bijvoorbeeld door het gemiddelde te nemen. Veel woorden voor de definitie van de tijdreeks \(y_n\) als \[y_n=\frac{1}{2q+1}(x_{n-q}+x_{n-q-1}+\cdots x_{n+q-1}+x_{n+q})=\frac{1}{2q+1}\sum_{k=-q}^{q}x_{n+k}\tiny.\] In praktijk wordt echter vaker het volgende gewogen voortschrijdend gemiddelde toegepast \[y_n=\sum_{k=-q}^{q}\binom{2q}{k+q}\cdot (\tfrac{1}{2})^{2q}\cdot x_{n+k}\] Als de filterbreedte \(q=1\) respectievelijk \(q=2\) betekent dit dat \(y_n=\tfrac{1}{4}\!x_{n-1}+\tfrac{1}{2}\!x_n+\tfrac{1}{4}\!x_{n+1}\) respectievelijk \(y_n=\tfrac{1}{16}\!x_{n-2}+\tfrac{1}{4}\!x_{n-1}+\tfrac{3}{8}\!x_n+\tfrac{1}{4}\!x_{n+1}+ \tfrac{1}{16}\!x_{n+2}\) is.
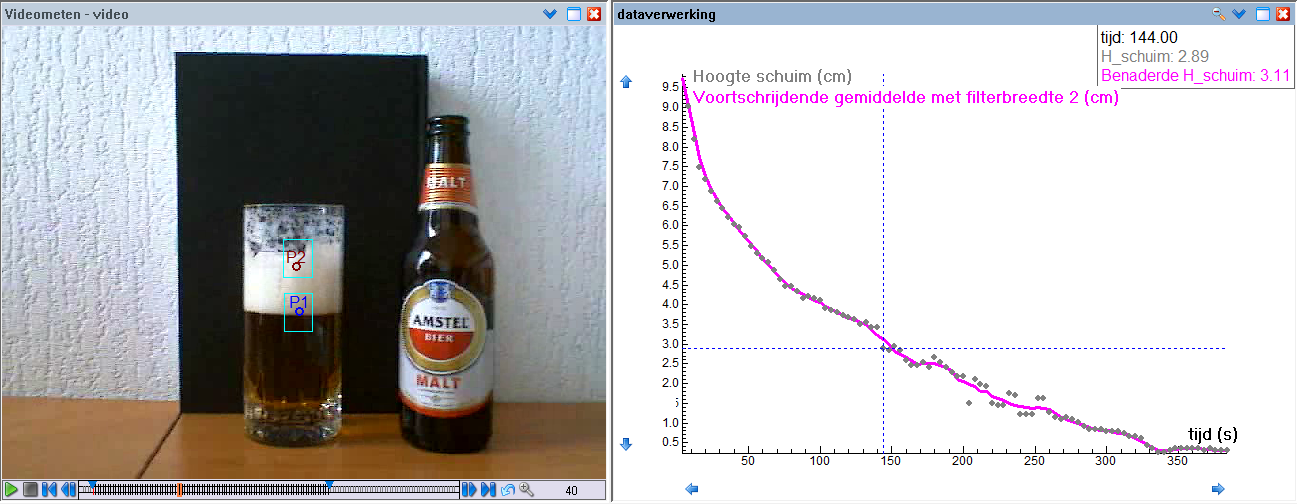
In onderstaande schermafdruk is een videometing van de schuimkraag van bier te zien samen met een filtering via het voortschrijdend gemiddelde met filterbreedte 2. Je ziet dat de meetgegevens een beetje gladgestreken worden, of anders gezegd, dat de meetfouten verwerkt worden.