Numeriek differentiëren: Tijdreeksen
 Kruiscorrelatie en convolutie van tijdreeksen
Kruiscorrelatie en convolutie van tijdreeksen
Het voortschrijdend gemiddelde is een voorbeeld van een lineair filter dat ontstaat door correlatie en convolutie van twee tijdreeksen. We leggen uit wat we hiermee bedoelen. Maar eerst eens twee definities.
Definities Als \(a_n\) en \(b_n\) tijdreeksen zijn dan is de kruiscorrelatie of kortweg correlatie van deze tijdreeksen, genoteerd als \(a\otimes b\), gedefinieerd door \[(a\otimes b)_n=\sum_k a_{n+k}b_k\]
Als \(a_n\) en \(b_n\) tijdreeksen zijn dan is de convolutie van deze tijdreeksen, genoteerd als \(a\ast b\), gedefinieerd door \[(a\ast b)_n=\sum_k a_{k}b_{n-k}\]
Kanttekening: in de vakliteratuur is er geen eenduidige definitie van correlatie en convolutie. Wij hebben de conventie zoals geïmplementeerd in de numpy module gehanteerd. Maar altijd gaat bij deze begrippen om een product van een tijdreeks met een andere verschoven tijdreeks. Onderstaande visualisatie voor de kruiscorrelatie \(\otimes\) illustreert dit.
We tekenen de tijdreeksen \(a_n\) en \(b_n\) horizontaal onder een getallenlijn voor gehele getallen. Als voorbeeld berekenen we \((a\otimes b)_2\).

Eigenschap De convolutie operator \(\ast\) is commutatief, d.w.z. \[a\ast b=b\ast a\] voor tijdreeksen \(a_n\) en \(b_n\).
Eigenschap De convolutie operator \(\ast\) is associatief, d.w.z. \[(a\ast b)\ast c=a\ast (b\ast c)\] voor tijdreeksen \(a_n\), \(b_n\) en \(c_n\).
Een filter als kruiscorrelatie Stel dat we een gewogen voortschrijdend gemiddelde met filterbreedte \(q\) en wegingen \(w_k\) met \(k=-q, -q+1, \ldots q-1, q\) toepassen op een tijdreeks \(x_n\). Dan krijgen we de nieuwe tijdreeks \[y_n=\sum_{k=-q}^q x_{n+k}w_{k}\] We kunnen de wegingen uitbreiden tot een tijdreeks \(w_n\) door \(w_n\stackrel{\text{def}}{=}0\) voor \(|n|>q\). Met andere woorden, we vullen links en rechts aan met nullen. Deze tijdreeks wordt de kern van het filter genoemd en de elementen ongelijk aan nul heten filtercoëfficiënten. Dan is bovenstaande som te herverschrijven als \[y_n=\sum_{k=-\infty}^{\infty} y_{n+k}w_{k}\] of kortweg \[y_n=\sum_{k} y_{n+k}w_{k}\] Maar dan mogen we schrijven dat de tijdreeks \(y\) gelijk is aan de kruiscorrelatie van de oorspronkelijke tijdreeks \(x\) en de kern \(w\) van het filter. Dus \[y=x \otimes w\]
Een filter als convolutie Gegeven de kern \(w\) van het lineaire filter definiëren we de geadjungeeerde van \(w\), genoteerd met \(w(-)\), door de filtercoefficiënten achterstevoren te plaatsen; met andere woorden \[w(-)_n=w_{-n}\] voor alle \(n\). Dan kunnen we het gewogen voorschrijdend gemiddelde ook schrijven als \[y_n=\sum_k y_{n+k}w_{k}=\sum_k y_{n-k}w(-)_k=\sum_k y_kw(-)_{n-k}\] Maar dan mogen we schrijven dat de tijdreeks \(y\) gelijk is aan de convolutie van de oorspronkelijke tijdreeks \(x\) en de geadjungeerde van \(w\). Dus: \[y=x \ast w(-)\]
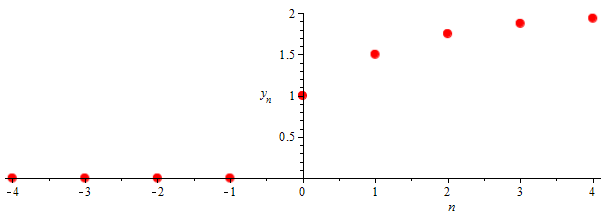
Voorbeeld 1 Stel dat \(r\) een vast gekozen getal met \(|r|<1\) is. We nemen de tijdreeksen \(x\) en \(w\) gedefinieerd door \[x_n=\left\{\begin{array}{ll} 1 & \text{als }n\ge 0\\ 0 & \text{als }n<0\end{array}\right.\] en \[w_n=\left\{\begin{array}{ll} 0 & \text{als }n> 0\\ r^{-n} & \text{als }n\le0\end{array}\right.\] Dan kunnen we de kruiscorrelatie \(y=x\otimes w\) en de convolutie \(y=x\ast w(-)\) bepalen: \[\begin{aligned}y_n& =(x \otimes w)_n= (x \ast w(-))_n=\sum_{k}x_kw(-)_{n-k}=\sum_{k}x_kw_{k-n}\\ &=\left\{\begin{array}{ll} 1+r+r^2+\cdots+r^n & \text{als }n\ge 0\\ 0 & \text{als }n<0\end{array}\right.\\ &=\left\{\begin{array}{ll} \frac{1-r^{n+1}}{1-r} & \text{als }n\ge 0\\ 0 & \text{als }n<0\end{array}\right.\end{aligned}\] In onderstaande grafiek van het gefilterde signaal voor \(r=\tfrac{1}{2}\) is ook te zien dat de waarde voor grote \(n\) convergeren naar \(\frac{1}{1-r}=2\).
Voorbeeld 2 Het berekenen van uitkomsten van filters kan gedaan via berekeningen met ijle matrices ('sparse matrices'). Onderstaande voorbeeld illustreert dit aan de hand van het gewogen voortschrijdend gemiddelde met filterbreedte \(1\) gedefinieerd door \[w_i=\left\{\begin{array}{ll} \tfrac{1}{4} & \text{als }|i|=1,\\ \tfrac{1}{2} & \text{als }i=0,\\ 0 & \text{anders}\end{array}\right.\] Behalve de discrete tijdreeks \(w\) kiezen we voor de tweede discrete tijdreeks \(x\) de rij gedefinieerd door \[x_i=\left\{\begin{array}{ll} 2i+1 & \text{als }i=0, 1, 2, 3\\ 0 & \text{anders}\end{array}\right.\] De tijdreeks \(y\) die ontstaat door kruiscorrelatie van de tijdreeksen \(x\) en \(w\) is dan gelijk aan \[y_i=(x\otimes w)_i = \left\{\begin{array}{ll} \tfrac{1}{4} & \text{als } i=-1 \\ \tfrac{5}{4} & \text{als } i=0 \\ 3 & \text{als } i=1 \\ 5 & \text{als } i=2 \\ \tfrac{19}{4} & \text{als } i=3 \\ \tfrac{7}{4} & \text{als } i=4 \\ 0 & \text{anders}\end{array}\right.\] Dit is op basis van definities uit te rekenen, maar ook via matrixvermenigvuldiging van ijle matrices (waarin we een coëfficiënt gelijk aan \(0\) nemen tenzij uitdrukkelijk anders gedefinieerd). We schrijven alleen een eindig deel van de tijdreeks \(x\) als kolomvector op en plaatsen de filtercoëfficiënten van \(w\) als rijen langs de hoofddiagonaal in een matrix zodanig dat alle niet-per-definite-nul-zijnde gefilterde waarden berekend kunnen worden; in dit geval doen we dit door \[\frac{1}{4}\cdot\left(\begin{array}{cccccc} 2 & 1 & & & & \\ 1 & 2 & 1 & & & \\ & 1 & 2 & 1 & & \\ & & 1 & 2& 1 & \\ & & & 1 & 2 & 1\\ & & & & 1 & 2\end{array}\right)\cdot\left(\begin{array}{c}0\\ 1 \\ 3\\ 5\\ 7 \\ 0\end{array}\right) = \frac{1}{4}\cdot\left(\begin{array}{c}1\\5 \\ 12\\ 20\\ 19 \\ 7\end{array}\right)= \left(\begin{array}{l}0.25\\1.25 \\ 3\\ 5 \\ 4.75 \\ 1.75\end{array}\right)\]
In Python wordt het rekenen met (ijle) matrices ondersteund in de numpy module en kun je de functie correlate als volgt aanroepen voor deze berekening via:
>>> import numpy as np
>>> np.correlate([1, 3, 5, 7], [0.25, 0.5, 0.25], "full")
array([ 0.25, 1.25, 3. , 5. , 4.75, 1.75])
Met andere worden, je rekent met eindige signalen via matrix-vectorvermenigvuldiging. Met de sleutelwoorden "same" respectievelijk valid" i.p.v "full" krijg je de voor een eindig ingangssignaal \(x\) een uitgangssignaal \(y\) met even veel waarden als het ingangssignaal respectievelijk met minder waarden omdat je randpunten niet uitrekent door denkbeeldige nullen toe te voegen aan het beginsignaal aan de rand.
>>> np.correlate([1, 3, 5, 7], [0.25, 0.5, 0.25], "same")
array([ 1.25, 3. , 5. , 4.75])
>>> np.correlate([1, 3, 5, 7], [0.25, 0.5, 0.25], "valid")
array([ 3. , 5.])
De convolutie van twee tijdreeksen kun je in Python bereken met de convolve functie. Omdat het gekozen filter in dit voorbeeld symmetrisch is krijg je hetzelfde resultaat:
>>> np.convolve([1, 3, 5, 7], [0.25, 0.5, 0.25], "full")
array([ 0.25, 1.25, 3. , 5. , 4.75, 1.75])


