We bekijken een signaal \(x_n\) voor \(i=1,\ldots\) en gaan na hoe exponentiële gladstrijking ('exponential smoothing') ruis kan verwijderen. We kunnen ons het signaal \(x\) voorstellen als uitgebreid met nullen voor negatieve gehele indices. Het begint met convolutie van dit signaal met het volgende signaal dat voor vaste keuze van \(\alpha\) tussen \(0\) en \(1\) gedefinieerd is door \[w_n=\left\{\begin{array}{ll} \alpha (1-\alpha)^n & \mathrm{voor\;}n=0,1,2,\ldots \\ 0 & \mathrm{anders}\end{array}\right.\] Voor de convolutie \(y=x\ast w\) kun je dan opschrijven: \[y_n=\alpha x_n+ \alpha (1-\alpha)x_{n-1}+\alpha (1-\alpha)^2x_{n-2}+\cdots + \alpha (1-\alpha)^nx_0\]

1. Toon aan dat de volgende recursierelatie geldt voor \(n>0\): \[y_n=\alpha x_n + (1-\alpha)y_{n-1}\]
2. Omdat \(y_0=\alpha x_0\) en \(y_n=0\) voor negatieve \(n\) kunnen we deze recursierelatie gebruiken om de convolutie voor elke index te berekenen als gewogen som van de ongefilterde waarde voor de gegeven index en de voorafgaande gefilterde waarde (voor de gegeven index minus 1). We maken dus een eigen convolutiefinctie en gebruiken niet die van Numpy.
   
   Schrijf een functie in de door jou gekozen programmeertaal die een gegeven eindig signaal filtert via exponentiële gladstrijking op basis van bovenstaande recursieformule bij gegeven parameter \(\alpha\). Pas jouw functie toe op de bierkraag gegevens uit het bijgevoegde excel sheet bierkraag.xlsx (hoogte bierkraag versus tijd) of bierkraag.csv (data gescheiden met puntkomma) voor drie verschillende waarden van \(\alpha\). Teken steeds de puntgrafiek van de meetgegevens en de kromme na filtering in één diagram en plaats de drie diagrammen pal onder elkaar voor vergelijking van de bereikte gladstrijking.
   
   Hieronder staat de grafiek na exponentiële gladstrijking. Je ziet dat het enige tijd duurt voor de gefilterde data bij de meetgegevens passen.

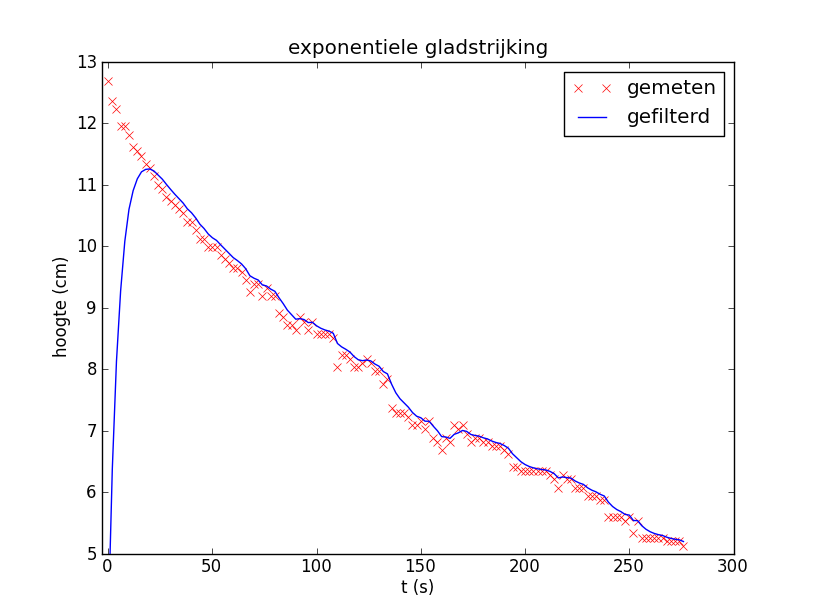
Om deze reden wordt de recursierelatie meestal niet gestart met \(y_0=\alpha x_0\), maar neemt men \(y_0= x_0\) of kiest men voor \(y_0\) de gemiddelde waarde van de eerste paar meetpunten. Hieronder staat de grafiek van filtering met startwaarde gelijk gekozen aan het gemiddelde van de eerste vijf meetgegevens

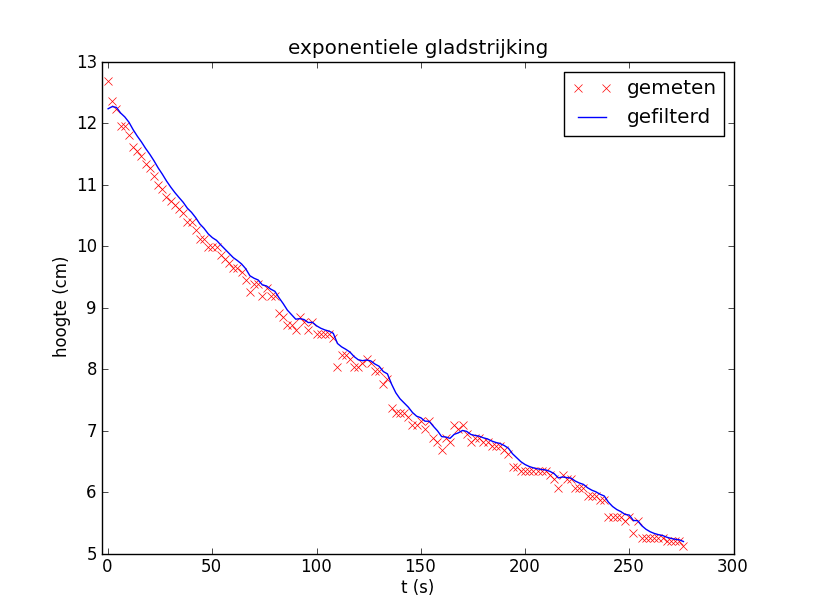
Als je de indruk hebt dat de gefilterde grafiek enigszins rechts van de dataplot ligt, of anders gezegd dat de gefilterde data groter zijn dan de gemeten data, dan kan dit kloppen. Bij dalende grafieken is dat altijd zo omdat de exponentiële filtering tegen probeert te gaan dat je van de tot dan toe berekende waarden weg loopt. Bij stijgende grafieken zou je het tegenovergestelde zien: dan zijn gefilterde data kleiner dan de gemeten data. Hiervan kan je gebruik maken door niet alleen de data in voorwaartse richting te filteren, maar ook achterwaarts beginnend bij het laatste meetpunt. Hieronder staat de grafiek van achterwaartse filtering.

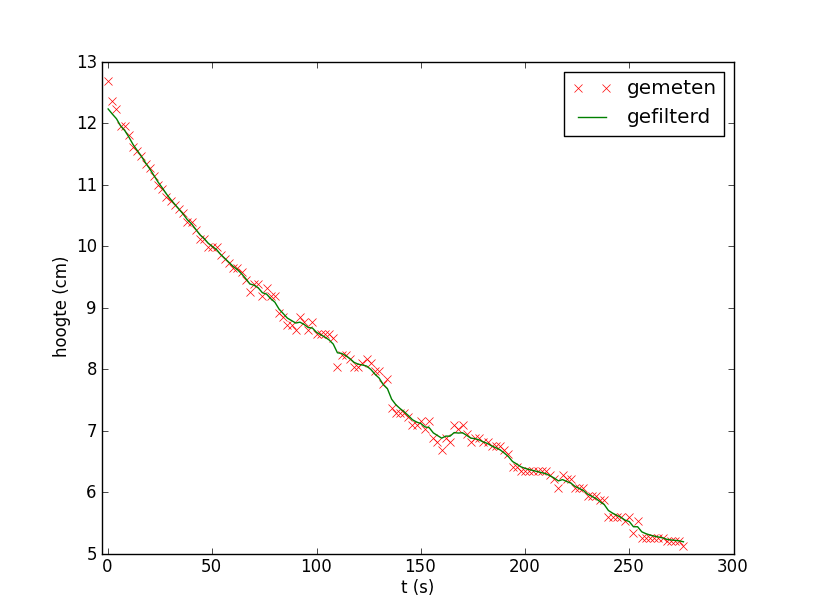
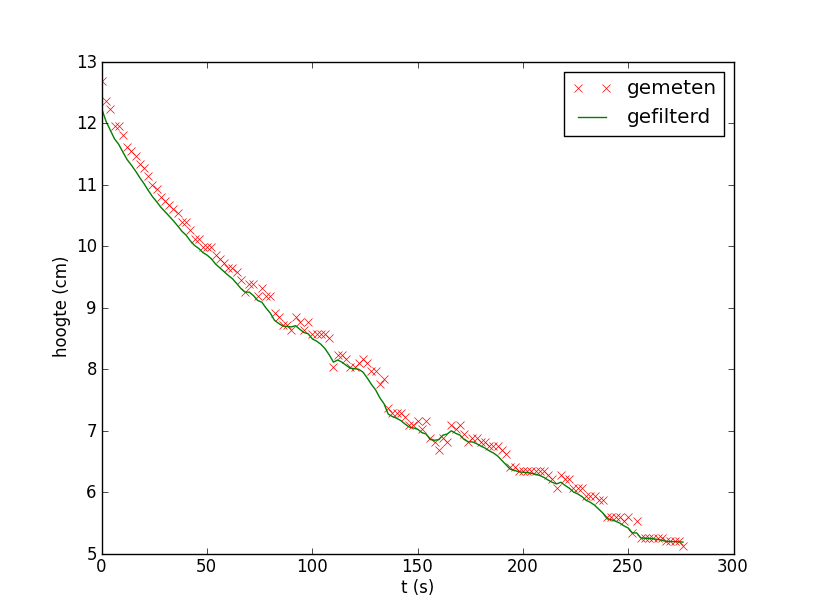Door beide gefilterde signalen te middelen krijg je dus een beter resultaat.

3. Implementeer deze aan aanpak en zie dat je een grafiek krijgt die lijkt op onderstaand resultaat:

4. Probeer je functie voor exponentiële filtering ook eens uit op een sinusgrafiek met ruis over het interval \((0,\pi)\).