Numerical differentiation: Difference formulas for the first derivative
 Simple difference formulas
Simple difference formulas
For a 'neat' function \(f(x)\) and a certain step size \({\vartriangle}x\), we have according to Taylor's theorem about \(x_0\) \[f(x_0+{\vartriangle}x)=f(x_0)+f'(x_0){\vartriangle}x+\tfrac{1}{2}f''(\xi)({\vartriangle}x)^2\] for some \(\xi\) between \(x_0\) and \(x_0+{\vartriangle}x\). We write down the forward difference \[{\vartriangle}f(x_0)=f(x_0+{\vartriangle}x)-f(x)\] and thus have the formula \[\frac{{\vartriangle}f(x_0)}{{\vartriangle}x}=f'(x_0)+\tfrac{1}{2}f''(\xi){\vartriangle}x\] for some \(\xi\) between \(x_0\) and \(x_0+{\vartriangle}x\). The left-hand side is called the forward difference quotient in \(x_0\) with step size \({\vartriangle}x\).
The formula also means that if the function values for \(x_0\) and \(x_0+{\vartriangle}x\) are known, the derivative \(f'(x_0)\) can be approximated with the forward difference quotient and the truncation error is given by \(\tfrac{1}{2}f''(\xi){\vartriangle}x\) for some \(\xi\) between \(x_0\) and \(x_0+{\vartriangle}x\). You often read this result as the following formula of forward difference.
Formula of forward difference \[f'(x_0)\approx \frac{f(x_0+h)-f(x_0)}{h},\quad \text{for a small positive value of }h\text.\]
The figure below illustrates the idea of forward difference as an approximation of a derivative.
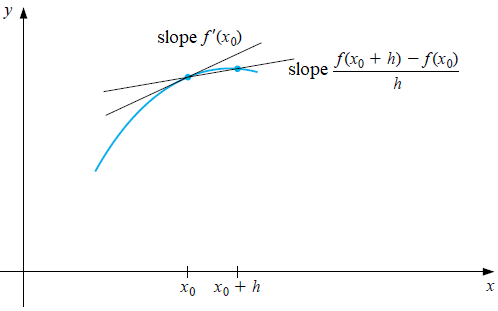
In a similar way you can define backward difference and arrive at the formula below.
Formula of backward difference \[f'(x_0)\approx \frac{f(x_0)-f(x_0-h)}{h},\quad \text{for a small positive value of }h\text.\]
The accuracy of the backward difference quotient is comparable to that of the forward difference quotient.
We consider \(f(x)=\ln x\) and \(x_0=2.0\). We know the first and second derivative: \(f'(x)=\frac{1}{x},\quad f''(x)=-\frac{1}{x^2}\). So we can compare numerical approximations of the derivative \(f'(x_0)\) via the forward and backward difference quotient with the exact value \(f'(x_0)=\tfrac{1}{2}\). With the forward difference quotient for \(\xi\) between \(x_0\) and \(x_0+h\) we find that \[|\tfrac{1}{2}f''(\xi)h|=|-\frac{h}{2\xi^2}|\le \frac{h}{8}\] The absolute value of the truncation error is therefore less than or equal to \(\frac{h}{8}\).
The table below shows for the different step sizes \(h\) the approximation of \(f'(x_0)\) with the forward difference quotient, the absolute value of the truncation error, and its upper estimate. \[\begin{array}{l|c|c|l} h & \frac{f(x_0+h)-f(x_0)}{h} & |\mathit{truncation\;error}| & \frac{h}{8} \\ \hline 0.5 & 0.44628710 & 0.05371290 & 0.0625 \\
0.4 & 0.45580389 & 0.04419611 & 0.0500 \\
0.3 & 0.46587314 & 0.03412686 & 0.0375 \\
0.2 & 0.47655090 & 0.02344910 & 0.0250 \\
0.1 & 0.48790164 & 0.01209836 & 0.0125 \\
0.05 & 0.49385225 & 0.00614775 & 0.00625 \\
0.01 & 0.49875415 & 0.00124585 & 0.00125 \\
0.001 & 0.49987504 & 0.00012496 & 0.000125 \\
0.0001 & 0.49998750 & 0.00001250 & 0.0000125 \\
0.00001 & 0.49999875 & 0.00000125 & 0.00000125 \\ \end{array}\]
With the backward difference quotient for \(\xi\) between \(x_0-h\) and \(x_0\) we find that \[|\tfrac{1}{2}f''(\xi)h|=|-\frac{h}{2\xi^2}|\le \frac{h}{2(x_0-h)^2}\] So the absolute truncation error at step size \(h\) is less than or equal to \(\frac{h}{2(x_0-h)^2}\).
We then get the table below. \[\begin{array}{l|c|c|c} h & \frac{f(x_0)-f(x_0-h)}{h} & |\mathit{truncation\;error}| & \frac{h}{2(x_0-h)^2} \\ \hline
0.5 & 0.57536414 & 0.07536414 & 0.11111111\\
0.4 & 0.55785888 & 0.05785888 & 0.07812500\\
0.3 & 0.54172976 & 0.04172976 & 0.05190311\\
0.2 & 0.52680258 & 0.02680258 & 0.03086420\\
0.1 & 0.51293294 & 0.01293294 & 0.01385042\\
0.05 & 0.50635616 & 0.00635616 & 0.00657462\\
0.01 & 0.50125418 & 0.00125418 & 0.00126259\\
0.001 & 0.50012504 & 0.00012504 & 0.00012513\\
0.0001 & 0.50001250 & 0.00001250 & 0.00001250\\
0.00001 & 0.50000125 & 0.00000125 & 0.00000125\\ \end{array}\]


