Numeriek differentiëren: Differentieformules voor de eerste afgeleide
 Eenvoudige differentieformules
Eenvoudige differentieformules
Voor een 'nette' functie \(f(x)\) en een zekere stapgrootte \({\vartriangle}x\) geldt volgens de steling van Taylor rondom \(x_0\) \[f(x_0+{\vartriangle}x)=f(x_0)+f'(x_0){\vartriangle}x+\tfrac{1}{2}f''(\xi)({\vartriangle}x)^2\] voor zekere \(\xi\) tussen \(x_0\) en \(x_0+{\vartriangle}x\). We noteren de voorwaartse differentie \[{\vartriangle}f(x_0)=f(x_0+{\vartriangle}x)-f(x)\] en hebben dus de formule \[\frac{{\vartriangle}f(x_0)}{{\vartriangle}x}=f'(x_0)+\tfrac{1}{2}f''(\xi){\vartriangle}x\] voor zekere \(\xi\) tussen \(x_0\) en \(x_0+{\vartriangle}x\). De linkerkant heet het voorwaartse differentiequotiënt in \(x_0\) met stapgrootte \({\vartriangle}x\).
De formule betekent ook dat als de functiewaarden voor \(x_0\) en \(x_0+{\vartriangle}x\) bekend zijn, de afgeleide \(f'(x_0)\) benaderd kan worden met het voorwaartse differentiequotiënt en dat de afbreekfout gegeven wordt door \(\tfrac{1}{2}f''(\xi){\vartriangle}x\) voor zekere \(\xi\) tussen \(x_0\) en \(x_0+{\vartriangle}x\). Je leest dit resultaat vaak als de volgende formule van voorwaartse differentie
Formule van voorwaartse differentie \[f'(x_0)\approx \frac{f(x_0+h)-f(x_0)}{h},\quad \text{voor een kleine positieve waarde van }h\text.\]
Onderstaande figuur illustreert het idee van voorwaartse differentie als benadering van een afgeleide.
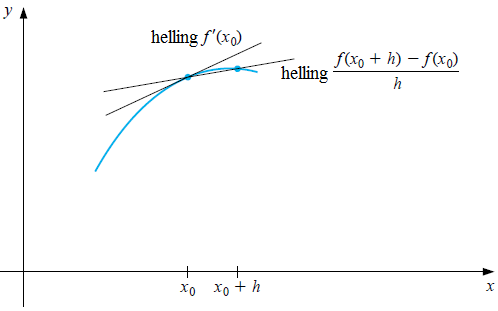
Op soorthelijke wijze kun je achterwaartse differentie definiëren en uitkomen op de onderstaande formule.
Formule van achterwaartse differentie \[f'(x_0)\approx \frac{f(x_0)-f(x_0-h)}{h},\quad \text{voor een kleine positieve waarde van }h\text.\]
De nauwkeurigheid van het achterwaartse differentiequotiënt is vergelijkbaar met die van het voorwaartse differentiequotiënt.
We nemen \(f(x)=\ln x\) en \(x_0=2.0\). Dan kennen we de eerst een tweede afgeleide: \(f'(x)=\frac{1}{x},\quad f''(x)=-\frac{1}{x^2}\). Dus kunnen we numerieke benaderingen van de afgeleide \(f'(x_0)\) via het voorwaartse en achterwaartse differentiequotiënt met de exacte waarde \(f'(x_0)=\tfrac{1}{2}\) vergelijken. Bij het voorwaartse differentiequotiënt geldt voor \(\xi\) tussen \(x_0\) en \(x_0+h\) dat \[|\tfrac{1}{2}f''(\xi)h|=|-\frac{h}{2\xi^2}|\le \frac{h}{8}\] De absolute waarde van de afbreekfout is dus bij stapgrootte \(h\) kleiner dan of gelijk aan \(\frac{h}{8}\).
In onderstaande tabel staan voor de verschillende stapgroottes \(h\) de benadering van \(f'(x_0)\) met het voorwaartse differentiequotiënt, de absolute waarde van de afbreekfout en de bovenschatting hiervan. \[\begin{array}{l|c|c|l} h & \frac{f(x_0+h)-f(x_0)}{h} & |\mathit{afbreekfout}| & \frac{h}{8} \\ \hline 0.5 & 0.44628710 & 0.05371290 & 0.0625 \\
0.4 & 0.45580389 & 0.04419611 & 0.0500 \\
0.3 & 0.46587314 & 0.03412686 & 0.0375 \\
0.2 & 0.47655090 & 0.02344910 & 0.0250 \\
0.1 & 0.48790164 & 0.01209836 & 0.0125 \\
0.05 & 0.49385225 & 0.00614775 & 0.00625 \\
0.01 & 0.49875415 & 0.00124585 & 0.00125 \\
0.001 & 0.49987504 & 0.00012496 & 0.000125 \\
0.0001 & 0.49998750 & 0.00001250 & 0.0000125 \\
0.00001 & 0.49999875 & 0.00000125 & 0.00000125 \\ \end{array}\]
Bij het achterwaartse differentiequotiënt geldt voor \(\xi\) tussen \(x_0-h\) en \(x_0\) dat \[|\tfrac{1}{2}f''(\xi)h|=|-\frac{h}{2\xi^2}|\le \frac{h}{2(x_0-h)^2}\] De absolute afbreekfout is dus bij stapgrootte \(h\) kleiner dan of gelijk aan \(\frac{h}{2(x_0-h)^2}\).
We krijgen dan onderstaande tabel. \[\begin{array}{l|c|c|c} h & \frac{f(x_0)-f(x_0-h)}{h} & |\mathit{afbreekfout}| & \frac{h}{2(x_0-h)^2} \\ \hline
0.5 & 0.57536414 & 0.07536414 & 0.11111111\\
0.4 & 0.55785888 & 0.05785888 & 0.07812500\\
0.3 & 0.54172976 & 0.04172976 & 0.05190311\\
0.2 & 0.52680258 & 0.02680258 & 0.03086420\\
0.1 & 0.51293294 & 0.01293294 & 0.01385042\\
0.05 & 0.50635616 & 0.00635616 & 0.00657462\\
0.01 & 0.50125418 & 0.00125418 & 0.00126259\\
0.001 & 0.50012504 & 0.00012504 & 0.00012513\\
0.0001 & 0.50001250 & 0.00001250 & 0.00001250\\
0.00001 & 0.50000125 & 0.00000125 & 0.00000125\\ \end{array}\]


