We have already considered the forward and backward difference quotient as an approximation for the first derivative of a 'neat' function \(f\) in \(x_0\). In an earlier example you have already seen that the truncation errors in these methods have opposite signs. This might give you the idea of averaging the formulas so that the errors cancel out as much as possible. The result of the averaging is known as the central difference.

The figure below illustrates the idea of central difference as an approximation of a derivative.

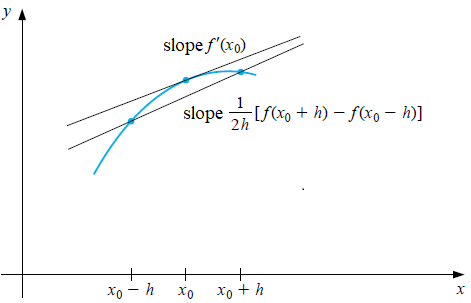
This gives indeed an approximation, but to understand this better we need to make the construction a bit more formal.

We look at two Taylor approximations about \(x_0\): \[\begin{aligned} f(x_0+h)=f(x_0)+f'(x_0)h+\tfrac{1}{2}f''(x_0)h^2+\tfrac{1}{6}f'''(x_0)h^3+ O(h^4)\\[3pt] f(x_0-h)=f(x_0)-f'(x_0)h+\tfrac{1}{2}f''(x_0)h^2-\tfrac{1}{6}f'''(x_0)h^3+ O(h^4)\end{aligned}\] When we subtract the second equation from the first, we get: \[ f(x_0+h)- f(x_0-h)=2f'(x_0)h+ \tfrac{1}{3}f'''(x_0)h^3 +O(h^4)\] or \[\frac{f(x_0+h)- f(x_0-h)}{2h}=f'(x_0)+ \tfrac{1}{6}f'''(x_0)h^2 +O(h^3)\] The truncation error for forward and backward difference was linear in \(h\), but the truncation error of the central difference approximation is quadratic in \(h\). This leads to a better approximation (when using larger \(h\)) for the central difference method than in the case of a forward or backward difference approximation. But as with the previous methods, the step size cannot be taken too small, because then rounding errors will play an annoying role.