We hebben al het voorwaartse en achterwaarste differentiequotiënt als benadering voor de eerste afgeleide van een 'nette' functie $f$ in $x_0$ bekeken. In een eerder voorbeeld heb je al kunnen zien dat de afbreekfouten in deze methoden tegengesteld teken hebben. Dit zou je op het idee kunnen brengen om de formules te middelen zodat de fouten zoveel mogelijk tegen elkaar wegvallen. Het resultaat van de middeling staat bekend als centrale differentie.

Onderstaande figuur illustreert het idee van centrale differentie als benadering van een afgeleide.

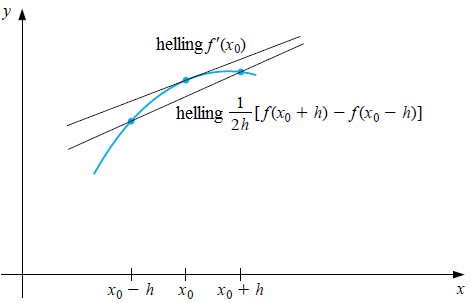
Dit geeft inderdaad een benadering, maar om dit goed te begrijpen moeten we de constructie wat formeler doen.

We bekijken twee Taylorbenaderingen rondom $x_0$:

$$\begin{aligned} f(x_0+h)=f(x_0)+f'(x_0)h+\tfrac{1}{2}f''(x_0)h^2+\tfrac{1}{6}f'''(x_0)h^3+ O(h^4)\\[3pt] f(x_0-h)=f(x_0)-f'(x_0)h+\tfrac{1}{2}f''(x_0)h^2-\tfrac{1}{6}f'''(x_0)h^3+ O(h^4)\end{aligned}$$ Trekken we de tweede vergelijking van de eerste af, dan krijgen we: $$f(x_0+h)- f(x_0-h)=2f'(x_0)h+ \tfrac{1}{3}f'''(x_0)h^3 +O(h^4)$$ oftewel $$\frac{f(x_0+h)- f(x_0-h)}{2h}=f'(x_0)+ \tfrac{1}{6}f'''(x_0)h^2 +O(h^3)$$ Was de afbreekfout bij voorwaartse en achterwaartse differentie nog lineair in $h$, bij centrale differentiatie is de afbreekfout kwadratisch in $h$. Dit levert een betere benadering op bij minder kleine $h$ voor de centrale differentiatie dan in het geval van voor- of achterwaartse differentie. Maar net als bij de eerdere methoden kan de stapgrootte niet te klein genomen worden omdat dan afrondfouten een vervelende rol gaan spelen.