When data are not smooth, the noise will increase as higher derivatives are numerically approximated. We consider this for the case of a known function \(f(x)=x^2\) on the interval \([-1,1]\). The first derivative is a straight line with slope 2 and the second derivative is the constant function 2.

We take 31 equidistant points on this interval and distort each function value by adding a randomly drawn number between \(-0.001, 0.001)\). We then compute numerical 1st and 2nd derivatives and compare the results with the exact values.

1. Figure out how to define the 5-point central difference formula for the first and second derivative in terms of convolution and use this to program two functions to calculate the derivatives (omit the edge points where the formula is not applicable).
   
   
2. Construct the noisy data as described above and apply your derivative functions to it.
   
   
3. Plot the graphs of the data and their 1st and 2nd numerical derivatives in one diagram. It can look like this:
   
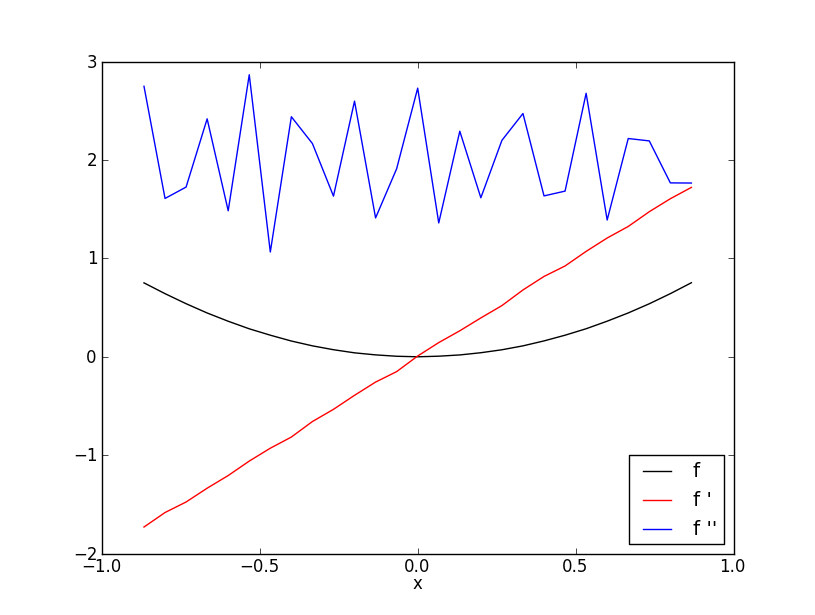
   The data graph still closely resembles a parabola. The graph of the first derivative still looks like a straight line. But the graph of the second derivative fluctuates around the constant value 2.
   
   
4. See what happens when you take 101 noisy data points.

Moral: With numerical derivatives, noise is a serious problem and data smoothing is usually a must; moreover, you should not choose a too small step size for difference formulas.