Wanneer data verstoord zijn dan zal de ruis bij het benaderen van afgeleiden toenemen naarmate er hogere afgeleiden benaderd worden. We bekijken dit voor het geval van een bekend functie \(f(x)=x^2\) op het interval \([-1,1]\). De eerste afgeleide is een rechte lijn met richtingscoëfficiënt 2 en de tweede afgeleide is de constante functie 2.

We nemen 31 equidistante punten op dit interval en verstoren elke functiewaarde door er een willekeurig getrokken getal tussen \(-0.001, 0.001)\) bij op te tellen. Vervolgens berekenen we numerieke 1ste en 2de afgeleiden en vergelijken de resultaten met de exacte waarden.

1. Bedenk hoe je de 5-punts centrale differentieformule voor de eerste en tweede afgeleide kunt definiëren in termen van convolutie en gebruik dit om twee functies in Python te programmeren om de afgeleiden te berekenen (laat de randpunten waar de formule niet toepasbaar is weg).
   
   
2. Construeer de verstoorde data zoals hierboven beschreven en pas hierop je functies om de afgeleiden uit te rekenen toe.
3. Teken de grafieken van de data en hun 1ste en 2de numerieke afgeleide in één figuur. Deze kan er als volgt uitzien:
   
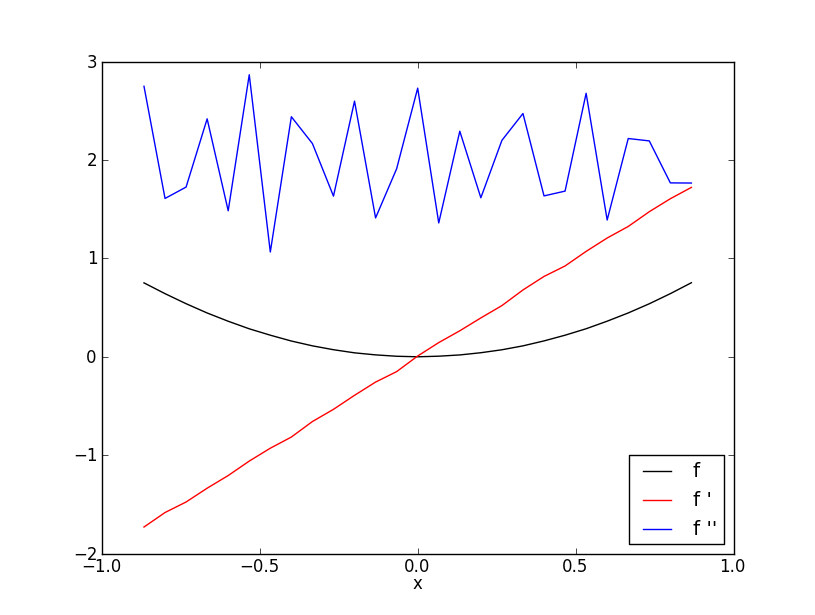
   De datagrafiek lijkt nog sterk op een parabool. De grafiek van de eerste afgeleide lijkt nog op een rechte lijn. Maar de grafiek van de tweede afgeleide schommelt om de constante waarde 2 in.
4. Kijk eens wat er gebeurt als je 101 verstoorde datapunten neemt.

Moraal: bij numeriek afgeleiden is ruis een serieus te nemen probleem en gladstrijken van data is meestal een must; bovendien mag je de stapgrootte voor differentieformules niet te klein kiezen.