In de biomechanica literatuur wordt de volgende dataset Pezzack.txt van Pezzack vaak gebruikt als benchmark voor dataverwerking. Het gaat om een videometing van een draaiing van een staaf in de ruimte en de hoekversnelling is ook analoog gemeten.

De volgende Python code kan gebruikt worden om de data in te lezen en de grafiek van de hoek en de versnelling te tekenen

import numpy as np
import matplotlib.pyplot as plt
tijd, hoek, hoek2, a_analoog = np.loadtxt('Pezzack.txt', skiprows=6, unpack=True)
plt.figure(figsize=(11,4))
plt.suptitle("Pezzack's benchmark data", fontsize=20)
plt.subplot(1,2,1)
plt.plot(tijd, hoek, 'b-')
plt.xlabel('tijd (s)', fontsize=12)
plt.ylabel('hoek (rad)', fontsize=12)
plt.subplot(1,2,2)
plt.plot(tijd, a_analoog, 'g-')
plt.xlabel('tijd (s)')
plt.ylabel('versnelling (rad/s$^2$)', fontsize=12)
plt.subplots_adjust(wspace=0.3)
plt.show()

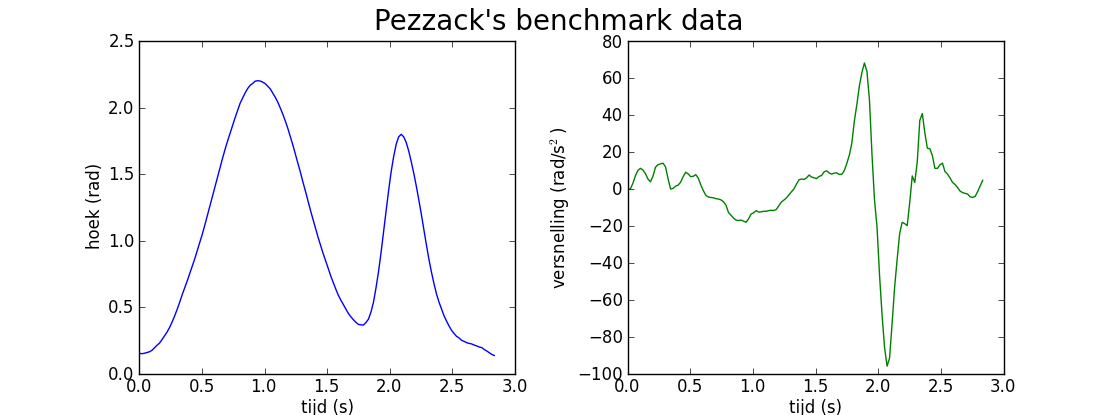
In andere programmeertalen kun je bovenstaande ook implementeren.

Gebruik de 3-punts centrale differentieformule voor de tweede afgeleide om de versnelling numeriek te benaderen en teken de grafiek van de benaderde versnelling samen met de grafiek van de analoog gemeten versnelling in één figuur.

Als alles goed gaat ziet kan het diagram er als volgt uit zien:

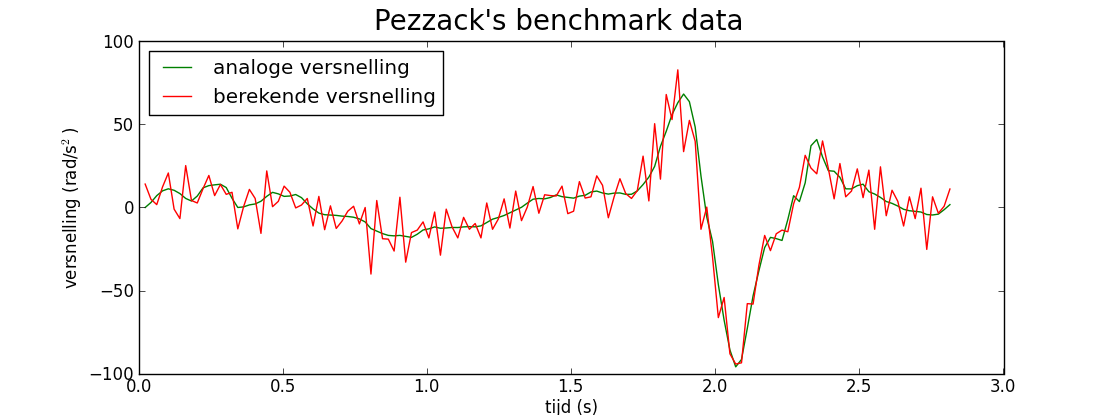
Wil je betere resultaten, dan moeten geavanceerdere methoden toegepast worden zoals Savitsky-Golay filtering of nog beter de 'cross-validatory penalized quintic spline smoothing' techniek.