Héron of Alexandria, an Egyptian mathematician from the first century AD, devised the following iterative method to accurately approximate the number $\sqrt{2}$. The idea is that a square of side $\sqrt{2}$ an area of $2$ and you can repeatedly make rectangles of area $2$ that increasingly resemble a square; see the figure below and the description of the construction.

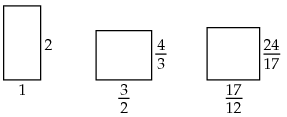
We start with a rectangle of width $b_0=1$ and length $l_0=2$. The following rectangle is created by taking the average width of the two sides of the first one: $b_1=\frac{b_0+l_0}{2}$. In order for the area of the rectangle to be formed to be equal to two, we need to take $l_1=\frac{2}{b_1}$ for the length. In numbers: $b_1=\frac{3}{2}, l_1=\frac{4}{3}$. You can repeat this procedure: the subsequent rectangle has width $b_2=\frac{b_1+l_1}{2}=\frac{17}{12}$ and length $l_2=\frac{2}{b_2}=\frac{24}{27}$. The sequence $b_0, b_1, b_2,\ldots$ converges to $\sqrt{2}$. You can easily prove that the value of $b_{n+1}$ depends on that of $b_n$ in the following way: $b_{n+1}=\frac{b_n}{2}+\frac{1}{b_n}$. In other words, $\sqrt{2}$ is a fixed point of the function

Assignment

1. Write a computer program that calculates the sequence of numbers resulting from function iteration with the function $f$ and starting value $x_0=1.0$.
   
   
2. Let $\epsilon_n$ the relative truncation error after $n$ iterations, i.e., $$\epsilon_n=\frac{x_n-\sqrt{2}}{\sqrt{2}}\tiny.$$ It can be shown that the following relationship holds between two successive relative truncation errors: $$\epsilon_{n+1}=\frac{\epsilon_n^2}{2(1+\epsilon_n)}$$ It is therefore plausible that for sufficiently large values of $n$ $$\epsilon_{n+1}=\tfrac{1}{2}\!\epsilon_n^2$$ So there is quadratic convergence in Héron's method. This means that for large $n$ the number of correct decimal places in the approximation doubles with each iteration step. The latter relation can also be converted to $$\frac{\epsilon_{n+1}}{2+\epsilon_{n+1}}=\left(\frac{\epsilon_{n}}{2+\epsilon_{n}}\right)^2$$ From this it can be deduced that for sufficiently large values of $n$ $$\epsilon_n\approx 2\left(\frac{\epsilon_0}{2+\epsilon_0}\right)^{2^n}$$ Use this formula and a calculator to estimate how many iterations are needed to get an approximation of $\sqrt{2}$ to 14 decimal places from a starting value of $x_0=1000$ accurate.
   
   Modify your computer program to experimentally verify the estimation.