Héron van Alexandrië, een Egyptische wiskundige uit de eerste eeuw van onze jaartelling, heeft de volgende iteratieve methode bedacht om het getal \(\sqrt{2}\) nauwkeurig te benaderen. Het idee is dat een vierkant met zijde \(\sqrt{2}\) een oppervlakte van grootte \(2\) heeft en dat je herhaald rechthoeken met oppervlakte \(2\) kunt maken die steeds meer op een vierkant gaan lijken; zie onderstaande figuur en de beschrijving van de constructie.

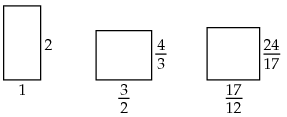
We beginnen met een rechthoek met breedte \(b_0=1\) en lengte \(l_0=2\). De volgende recht­hoek ontstaat door als breedte het gemiddelde te nemen van de twee zijden van de eerste: \(b_1=\frac{b_0+l_0}{2}\). Opdat de oppervlakte van de te vormen rechthoek gelijk is aan twee, moeten we voor de lengte nemen \(l_1=\frac{2}{b_1}\). In getallen: \(b_1=\frac{3}{2}, l_1=\frac{4}{3}\). Deze werk­wijze kun je herha­len: de volgen­de rechthoek heeft breedte \(b_2=\frac{b_1+l_1}{2}=\frac{17}{12}\) en lengte \(l_2=\frac{2}{b_2}=\frac{24}{27}\). De rij \(b_0, b_1, b_2,\ldots\) convergeert naar \(\sqrt{2}\). Je kunt eenvoudig bewijzen dat de waarde van \(b_{n+1}\) op de volgende manier van die van \(b_n\) afhangt: \(b_{n+1}=\frac{b_n}{2}+\frac{1}{b_n}\). Met andere woorden, \(\sqrt{2}\) is een dekpunt van de functie \[f(x)=\frac{x}{2}+\frac{1}{x}\] en de waarde is te benaderen d.m.v. iteratie van \(f\).

\(\phantom{x}\)

Opdracht

1. Schrijf een computerprogramma dat de rij getallen berekend die ontstaat uit functie-iteratie met de functie \(f\) en startwaarde \(x_0=1.0\).
   
   
2. Laat \(\epsilon_n\) de relatieve afbreekfout zijn na \(n\) iteraties, d.w.z \[\epsilon_n=\frac{x_n-\sqrt{2}}{\sqrt{2}}\tiny.\] Aangetoond kan worden dat het volgende verband tussen twee opeenvolgende relatieve afbreekfouten geldt: \[\epsilon_{n+1}=\frac{\epsilon_n^2}{2(1+\epsilon_n)}\] Het is dus aannemelijk dat voor voldoende grote waarden van \(n\) geldt dat \[\epsilon_{n+1}=\tfrac{1}{2}\epsilon_n^2\] Er is dus sprake van kwadratische convergentie in de methode van Héron. Dit betekent dat voor grote \(n\) het aantal correcte cijfers achter de komma in de benadering met elke iteratiestap verdubbelt. Het laatstgenoemde verband kan ook omgewerkt worden tot \[\frac{\epsilon_{n+1}}{2+\epsilon_{n+1}}=\left(\frac{\epsilon_{n}}{2+\epsilon_{n}}\right)^2\] Hieruit valt af te leiden dat voor voldoende grote waarden van \(n\) geldt \[\epsilon_n\approx 2\left(\frac{\epsilon_0}{2+\epsilon_0}\right)^{2^n}\] Gebruik deze formule en een rekenmachine om te schatten hoeveel iteraties nodig zijn om vanuit een startwaarde \(x_0=1000\) een benadering van \(\sqrt{2}\) te krijgen in 14 decimalen nauwkeurig.
   
   Pas je computerprogramma aan om de afschatting experimenteel te verifiëren.