Iteration of functions: Finding zeros via the Newton-Raphson method
 Deriving the Newton-Raphson method
Deriving the Newton-Raphson method
We show how the so-called Newton-Raphson method for finding zeros of a 'neat' function \(f\) follows from the theory of iteration of a functions.
To begin with, the equation \[f(x)=0\] is equivalent to \[x+\alpha\cdot f(x)=x\quad\text{provided }\alpha\neq 0\tiny.\] Instead of finding a zero of the function \(f\), we might as well try to approximate a fixed point of the iteration of the function \[g(x)=x+\alpha\cdot f(x)\] A fixed point \(s\) of \(g\) is attractive as \(|g'(s)| <1\) and we prefer to have \(|g'(s)|\) as small as possible. The best convergence therefore occurs when we choose \(\alpha\) such that \[1+\alpha\cdot f'(s)=0\] In other words, when we choose \[\alpha = -\frac{1}{f'(s)}\tiny.\]
The problem is, of course, that the fixed point \(s\) of the iteration of the function is not known in advance. A second observation is that we are free to choose a new \(\alpha\) in each iteration step, say \(\alpha_n\). If the function is 'neat', for example has a continuous derivative, then for a sequence \(x_0, x_1, x_2, \ldots\) that converges to a fixed point \(s\), also the sequence \(f'(x_0), f'(x_1), f'(x_2), \ldots\) will converge to \(f'(s)\). This motivates our choice to use in each step of the iteration the derivative of \(f\) in the iterand found at that moment to select the best \(\alpha\) via the formula \[\alpha_n=-\frac{1}{f'(x_n)}\] where \(x_n=g^n(x_0)\).
In this we have obtained the iterative formula for the Newton-Raphson method of finding zeros.
Newton-Raphson method For a function \(f\) with continuous derivative, a zero can be determined via the iteration \[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\] provided that the starting point \(x_0\) is chosen sufficiently close to a fixed point \(s\) and \(f'(s)\neq 0\).
Convergence behaviour of Newton-Raphson method The Newton-Raphson method for finding zeros of a function \(f\) is thus nothing more than the iteration of the function \[N(x)=x-\frac{f(x)}{f'(x)}\] with a starting value \(x_0\) sufficiently close to an attractive fixed point \(s\) with \(f'(s)\neq 0\). We have: \[N(s)=s,\quad N'(s)=0, \quad N''(s)= \frac{f''(s)}{f'(s)}\tiny.\] (Check the last equality yourself.) Now let's study the convergence behaviour of the Newton-Raphson method. Let \(\epsilon_n=x_n-s\) be the absolute truncation error of the \(n\)-th approximation to the fixed point \(s\). So \(x_n=s+\epsilon_n\). According to Taylor's theorem, there is a \(\xi\) between \(s\) and \(x_n\) such that \[N(x_n)=N(s)+N'(s)\cdot \epsilon_n+\tfrac{1}{2}\!N''(\xi)\cdot \epsilon_n^2\] In other words: \[x_{n+1}=s+\frac{f''(\xi)}{2f'(\xi)}\cdot \epsilon_n^2\] for some \(\xi\) between \(s\) and \(x_n\). In other words \[\epsilon_{n+1}=\frac{f''(\xi)}{2f'(\xi)}\cdot \epsilon_n^2\] and the convergence of the Newton-Raphson method is at least quadratic under the given circumstances.
We apply the Newton-Raphson method to the function \(f(x)=x^2-2\) to approximate \(\sqrt{2}\), starting in \(x_0=1\). Then the corresponding iteration function \(N(x)\) is given by \[N(x)=x-\frac{f(x)}{f'(x)}=x-\frac{x^2-2}{2x}=\frac{x}{2}+\frac{1}{x}\tiny.\] The Newton-Raphson method is now nothing else than Héron's method discussed earlier.
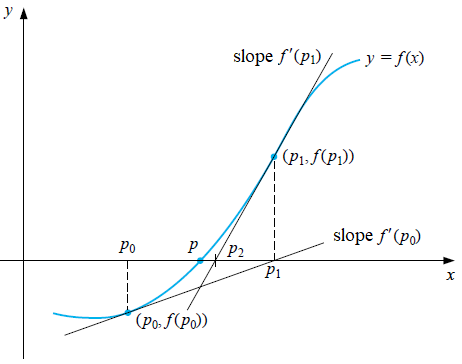
Graphic description of Newton-Raphson method The Newton-Raphson method for finding zeros of a function \(f\) can also be understood as follows, We start with an approximation \(x_0\) of a zero of \(f\). Determine the tangent to the graph from \(f\) in point \(\bigl(x_0, f(x_0)\bigr)\). Suppose that \(f'(x_0)\neq 0\), then this tangent intersects the \(x\)-axis at a point \(\bigl(x_1,0\bigr)\). We can calculate this point: the equation of the tangent line is \[y=f'(x_0)\cdot (x-x_0) +f(x_0)\] The \(x\)-coordinate of intersection of this line with the \(x\)-axis satisfies the equation \[f'(x_0)\cdot (x-x_0) +f(x_0)=0\] and is therefore equal to \[x_0-\frac{f(x_0)}{f'(x_0)}\] As next approximation of a zero of \(f\) we take \[x_1=x_0-\frac{f(x_0)}{f'(x_0)}\] and then we repeat this approximation process. The figure below illustrates the first two steps in this iteration process.