Functie-iteratie: Newton-Raphson methode van nulpuntsbepaling
 Afleiding van de Newton-Raphson methode
Afleiding van de Newton-Raphson methode
We laten zien hoe de zogenaamde Newton-Raphson methode voor nulpuntsbepaling van een 'nette' functie \(f\) uit de theorie van iteratie-functies ontstaat.
Om te beginnen is de vergelijking \[f(x)=0\] equivalent met \[x+\alpha\cdot f(x)=x\quad\text{mits }\alpha\neq 0\tiny.\] In plaats van een nulpunt van de functie \(f\) te bepalen, kunnen we net zo goed een dekpunt van de iteratie-functie \[g(x)=x+\alpha\cdot f(x)\] proberen te benaderen. Een dekpunt \(s\) van \(g\) is aantrekkend als \(|g'(s)| <1\) en het liefst hebben we \(|g'(s)|\) zo klein mogelijk. De beste convergentie treedt dus op bij de keuze van \(\alpha\) waarvoor geldt \[1+\alpha\cdot f'(s)=0\] oftewel wanneer \[\alpha = -\frac{1}{f'(s)}\tiny.\]
Probleem is natuurlijk dat het dekpunt \(s\) van de iteratie-functie vooraf niet bekend is. Een tweede observatie is dat het ons vrij staat om in iedere iteratiestap een nieuwe \(\alpha\) te kiezen, zeg \(\alpha_n\). Als de functie 'net' is, bijvoorbeeld een continue afgeleide heeft, dan zal bij een rij \(x_0, x_1, x_2, \ldots\) die naar een dekpunt \(s\) convergeert de rij \(f'(x_0), f'(x_1), f'(x_2), \ldots\) naar \(f'(s)\) convergeren. Dit motiveert onze keuze om in elke stap van de iteratie als geschikte \(\alpha\) de afgeleide van \(f\) in de op dat moment gevonden iterand te gebruiken via de formule \[\alpha_n=-\frac{1}{f'(x_n)}\] waarbij \(x_n=g^n(x_0)\).
We zijn zo uitgekomen bij de iteratieve formule voor de Newton-Raphson methode van nulpuntsbepaling.
Newton-Raphson methode Voor een functie \(f\) met continue afgeleide kan een nulpunt bepaald worden door de iteratie \[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\] mits het startpunt \(x_0\) voldoende dicht bij een dekpunt \(s\) gekozen wordt en \(f'(s)\neq 0\).
Convergentiegedrag van Newton-Raphson methode De Newton-Raphson methode voor nulpuntsbepaling van een functie \(f\) is dus niets anders dan de iteratie van de functie \[N(x)=x-\frac{f(x)}{f'(x)}\] met een startwaarde \(x_0\) voldoende dicht in de buurt van een aantrekkend dekpunt \(s\) met \(f'(s)\neq 0\). Er geldt: \[N(s)=s,\quad N'(s)=0, \quad N''(s)= \frac{f''(s)}{f'(s)}\tiny.\] (Ga de laatste gelijkheid zelf na.) Laten we nu eens het convergentiegedrag van de Newton-Raphson methode bestuderen. Laat \(\epsilon_n=x_n-s\) de absolute afbreekfout zijn van de \(n\)-de benadering van het dekpunt \(s\). Dus \(x_n=s+\epsilon_n\). Volgens de stelling van Taylor is er dan een \(\xi\) tussen \(s\) en \(x_n\) zodanig dat \[N(x_n)=N(s)+N'(s)\cdot \epsilon_n+\tfrac{1}{2}\!N''(\xi)\cdot \epsilon_n^2\] Anders gezegd: \[x_{n+1}=s+\frac{f''(\xi)}{2f'(\xi)}\cdot \epsilon_n^2\] voor zekere \(\xi\) tussen \(s\) en \(x_n\). Met andere woorden \[\epsilon_{n+1}=\frac{f''(\xi)}{2f'(\xi)}\cdot \epsilon_n^2\] en de convergentie van de Newton-Raphson methode is onder de gegeven omstandigheden dus minstens kwadratisch.
We passen de Newton-Raphson methode toe op de functie \(f(x)=x^2-2\) om \(\sqrt{2}\) te benaderen, waarbij we starten in \(x_0=1\). Dan is de bijpassende iteratie-functie \(N(x)\) gegeven door \[N(x)=x-\frac{f(x)}{f'(x)}=x-\frac{x^2-2}{2x}=\frac{x}{2}+\frac{1}{x}\tiny.\] De Newton-Raphson methode is nu niets ander dan de eerder besproken methode van Héron.
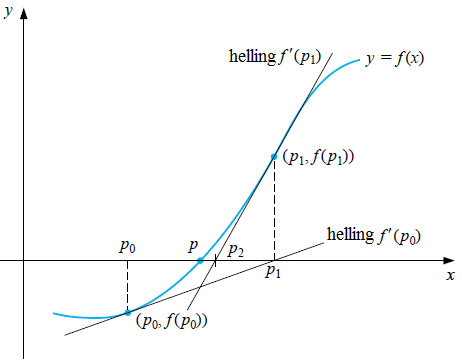
Grafische beschrijving van Newton-Raphson methode de Newton-Raphson methode voor de nulpuntsbepaling van een functie \(f\) kan ook als volgt begrepen worden, We beginnen met een benadering \(x_0\) van het nulpunt van \(f\). Bepaal de raaklijn aan de grafiek
van \(f\) in het punt \(\bigl(x_0, f(x_0)\bigr)\). Veronderstel dat \(f'(x_0)\neq 0\), dan snijdt deze raaklijn de \(x\)-as in een punt \(\bigl(x_1,0\bigr)\). Dit punt kunnen we uitrekenen: de vergelijking van de raaklijn is \[y=f'(x_0)\cdot (x-x_0) +f(x_0)\] De \(x\)-coördinaat van snijpunt van deze lijn met de \(x\)-as voldoet aan de vergelijking \[f'(x_0)\cdot (x-x_0) +f(x_0)=0\] en is dus gelijk aan \[x_0-\frac{f(x_0)}{f'(x_0)}\] Als volgende benadering van een nulpunt van \(f\) nemen we \[x_1=x_0-\frac{f(x_0)}{f'(x_0)}\] en hierna herhalen we dit benaderingsproces. Onderstaande figuur illustreert de eerst twee stappen in dit iteratieproces.