The bisection method is simple, but in general not very efficient, in part because only the sign of the function in the middle of a (sub)interval is used and not the size of the function value at this point. Useful information that could speed up the numerical method is ignored in this way. The regula falsi method, which is based on linear interpolation on the last calculated interval within which a zero point lies, does use this information.

Like the bisection method, the regula falsi method starts with an interval $[p_0,p_1]=[a,b]$ such that $f(a)\cdot f(b)<0$. But in this new method the centre is not chosen as the vertex of a new interval, but the function on $[a,b]$ is approximated with a linear interpolation function and the zero of this interpolation is chosen as the new approximation. In other words, the function is first approximated by the chord between the points $\bigl(a,f(a)\bigr)$ and $\bigl(b,f(b)\bigr)$, i.e. by the straight line with equation

$$y=\frac{f(b)-f(a)}{b-a}\cdot (x-b)+f(b)\tiny.$$ The intersection of this line has coordinates $(p_2,0)$ with $$p_2 = b-f(b)\cdot \frac{b-a}{f(b)-f(a)}\tiny.$$ If $p_2$ is a zero of the function $f$ you are done; if not, split the interval into left and right parts, $[a,p_2]$ $[p_2,b]$ respectively. At what interval the search for a zero continues depends on the sign of $f(p_2)$. If this sign is opposite to that of $f(a)$ choose the left interval, otherwise continue with the right interval. You repeat this halving process until you have encountered a zero or the change in the end points of the interval is smaller than a predetermined value. Note that the intervals in which you search for a zero point do not necessarily decrease in length. As an answer, you choose the centre of the last interval found as an approximation of the zero of the function. The figure below illustrates the first iterations in the halving method to find a zero point $p$ of a function $f$.

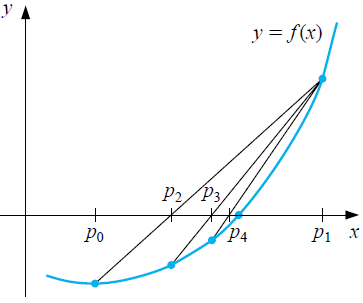
So what you get is a series of approximations of a zero

$$p_0, p_1, p_2, p_3, \ldots$$ that are getting closer and closer to each other. According to the above rule we stop as soon as (coincidentally) a zero point is found ( $f(p_n)=0$ for some $n$ ), or after $n$ steps if $$|p_n-p_{n-1}|<\epsilon$$ for a preselected tolerance $\epsilon$. In other words, we stop in the regula falsi method when the truncation error is less than the desired accuracy.

A disadvantage of the regula falsi method is that the approximation method does not converge as quickly as the sequence $p_1, p_2, p_3, \ldots$ is created by repeatedly adjusting the same side of the interval as in the figure above. The regula falsi method does not converge significantly faster or slower than the bisection method. But smart adjustments have been made to this method that do speed up the algorithm; we will not go into this.