The secant method resembles the regula falsi method in that the function $f$ is also linearly interpolated in every iteration step. But the difference is that there is no splitting of a search area. In fact, the starting point of the secant method need not be an interval at all within which a zero can be found.

We start in the secant method with two starting values $p_0=a$ and $p_1=b$ such that $f(p_1)\neq f(p_2)$. As in the regula falsi method, the function is first approximated by the chord between the points $\bigl(a,f(a)\bigr)$ and $\bigl(b,f(b)\bigr)$, i.e. by the straight line with equation $$y=\frac{f(b)-f(a)}{b-a}\cdot (x-b)+f(b)\tiny.$$ The intersection of this line has coordinates $(p_2,0)$ with $$p_2 = b-f(b)\cdot \frac{b-a}{f(b)-f(a)}\tiny.$$ If $p_2$ is a zero of the function $f$ you are done; otherwise repeat this process with the two points $[p_1, p_2]$. Then you get a new approximation via $$p_3 = p_2-f(p_2)\cdot \frac{p_2-p_1}{f(p_2)-f(p_1)}\tiny.$$ So we calculate with the recursion formula $$p_{n} = p_{n-1}-f(p_{n-1})\cdot \frac{p_{n-1}-p_{n-2}}{f(p_{n-1})-f(p_{n-2})},\quad p_0=a, p_1=b\tiny.$$ The figure below illustrates the first iterations in the secant method to find a zero point $p$ of a function $f$. For comparison with the regula falsi method, this has been added to the right for the drawn situation; the difference only shows up after two iteration steps.

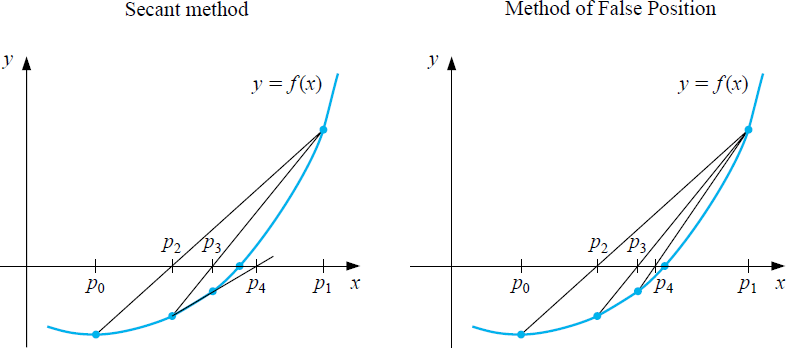
Because a zero is not sandwiched between two values in the secant method, there is no guarantee that the sequence $p_0, p_1, p_2, \ldots$ will converge to a zero. This is a disadvantage, but "every disadvantage has its advantage": the secant method works faster than the regula falsi method or the bisection method. Although the figure above does not suggest it, the secant method is more efficient than the regula false method. We can express this more formally as follows. If a sequence $p_1, p_2, p3, \ldots$ converges to the zero $p$ then the convergence of order $q$ when there is an interval around $p$ is such that for every beginning $p_1$ in this interval $|p_{n+1}-p|\le C\cdot |p_n-p|^q$, where $C<1$ as $q=1$. We speak of linear convergence and quadratic convergence when $q=1$ and $q=2$ respectively. For the regula falsi method it can be proven that convergence is linear, just like for the bisection method. But for the secant method, it can be proven that $q$ is equal to the golden ratio $q=\tfrac{1}{2}(1+\sqrt{5})\approx 1.619$. This means that convergence is substantially faster than in the linear case.