Introduction: structure of reasoning

Propositional Logic: Natural deduction

Introduction: structure of reasoning

Semantic vs syntactic perspective on argumentation In the previous section, a semantic perspective on the validity of an inference was discussed in terms of models. The formula \(\psi\) is herein a valid consequence of the formulas \(\phi_1, \ldots \phi_n \) if every model of the set \(\{\phi_1, \ldots \phi_n\}\) is also a model of \(\psi\). We denote this as \(\phi_1, \ldots \phi_n\vDash \psi\). This means that the formula \(\phi_1\land\ldots \phi_n\rightarrow \psi\) is a tautology.

However, this approach tells us little about how we arrive at a conclusion from a set of premises through reasoning. In other words, there is still a need for proving or deriving a conclusion based on accepted steps of reasoning. This is a syntactic perspective on the validity of a conclusion based on deductions that start with a set of premises. The formula \(\psi\) is now a conclusion that follows through a reasoning process involving accepted steps of inference, starting with formulas \(\phi_1, \ldots \phi_n \). We denote this as \(\phi_1, \ldots \phi_n\vdash \psi\). We also say that \(\psi\) can be derived from the formulas \(\phi_1, \ldots \phi_n \).

Note the distinction between \(\vDash\) and \(\vdash\). The symbol \(\vDash\) is associated with the semantic validity of an inference based on models. The symbol \(\vdash\) belongs to an inference that is derived through accepted steps of reasoning, starting from a set of given assumptions.

The following theorm states that the above-mentioned approaches to the validity of an inference, which have different natures, are in perfect agreement.

Correctness and completeness theorem If \(\Sigma\) is a set of logical formulas and \(\psi\) is a formula, then: \[\Sigma\vDash \phi\text{ if and only of }\Sigma\vdash \psi\]

The proof has two parts:

Completeness: (\(\Sigma\vDash \psi\) implies \(\Sigma\vdash \psi\))
There is a proof for every semantically valid inference.
Correctness: (\(\Sigma\vdash \psi\) implies \(\Sigma\vDash \psi\))
Derivable inferences are semantically valid.

We omit the proof of each of these parts as it is a bit too technical for this introduction.

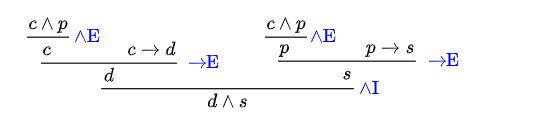
Let us use a concrete example to illustrate a derivation of a conclusion.

We assume the following information:

Claudia programs in C++ and Petra programs in Python.
If Claudia programs in C++, then the teacher is happy.
If Petra programs in Python, then the student assistant is happy.

These premises can lead to different sub-conclusions and these sub-conclusions, together with the premises, can lead to other sub-conclusions or can result in a final conclusion.

Step 1: premise 1 leads to 2 partial conclusions, one of which is:

1a. Claudia programs in C++.
After all, if Claudia is programming in C++ and Petra is programming in Python, then Claudia is definitely programming in C++.

Step 2: premise 2 and the sub-conclusion 1a lead to the sub-conclusion:

2a. The teacher is happy.
After all, according to 1a Claudia programs in C++, and the second premise states that if Claudia programs in C++, then the teacher is happy.

Step 3: premise 1 leads to 2 partial conclusions, one of these has been covered above, so we now look at the other:

1b. Petra programs in Python.
After all, if Claudia is programming in C++ and Petra is programming in Python, then Petra is definitely programming in Python.

Step 4: premise 3 and the sub-conclusion 1b lead to the sub-conclusion:

2b. The student assistant is happy.
After all, according to 2b, Petra programs in Python, and the second premise says that if Petra programs in Python, then the student assistant is happy.

Step 5: the sub-claims 2a and 2b can be combined into the following final conclusion:
c. The teacher is happy and the student assistant is happy.

In propositional language The above derivation can be described in propositional language as follows.

We use the following proposition variables:
\(c\) for "Claudia programs in C++."
\(p\) for "Petra programs in Python."
\(t\) for "the teacher is happy."
\(s\) for "the student assistant is happy."

Then we can write down three assumptions as logical formulas: \(c\land p\), \(c\rightarrow t\) and \(p\rightarrow s\).

The (partial) conclusions can also be written down in the form of logical formulas: \(\bigl(c\land p)\land (c\rightarrow t)\bigr)\rightarrow t\), \(\bigl((c\land p)\land (p\rightarrow s)\bigr)\rightarrow s\) and \(\bigl((c\land p)\land (c\rightarrow t)\land (p\rightarrow s)\bigr)\rightarrow (t\land s)\).

In the semantic approach with models you show that the formulas of the (sub-)conclusions are tautologies.

In the syntactic approach with derivations you show how to combine formulas using accepted derivation rules to reach (sub-)conclusions. In the remainder of this section, we are going to deal with the propositional language for derivation. However, we will give you below a sneak peek in advance.

From the formula \(c\land p\) we derive the formula \(c\) using the elimination rule for the conjunction. Then, by applying the elimination rule for implication, commonly known as Modus Ponens, to the formulas \(c\) and \(c\rightarrow t\), we obtain the formula \(t\). We can continue in this manner until we reach the final conclusion.

There are several notations in circulation to describe this process. One of them is (with the codes for the used inference rules in blue) the following tree structure:

Boomdiagram voor natuurlijke deductie

Another notation, which we will use henceforth, is the so-called Fitch notation:
\[\begin{array}{r|ll} 1 & c\land p & (\mathrm{P})\\ 2 & c\rightarrow d & (\mathrm{P})\\ 3 & p\rightarrow s & (\mathrm{P})\\ 4 & c & \land\,\mathrm{E}, 1 \\ 5 & d & \rightarrow\!\mathrm{E}, 2, 4\\ 6 & p & \land\,\mathrm{E}, 1\\ 7 & s & \rightarrow\!\mathrm{E}, 3, 6\\ 8 & d \land s & \land\,\mathrm{I}, 5, 7\end{array}\] Fitch notation is easier to handle for longer derivations.