Propositielogica: Natuurlijke deductie
Inleiding: structuur van redeneringen
Semantische vs syntactische blik op argumentatie In de vorige sectie is een semantische kijk op de geldigheid van een gevolgtrekking behandeld, in termen van modellen. De formule \(\psi\) is hierin een geldig gevolg van de formules \(\phi_1, \ldots \phi_n \) als elk model van de verzameling \(\{\phi_1, \ldots \phi_n\}\) ook een model is van \(\psi\). We noteren dit als \(\phi_1, \ldots \phi_n\vDash \psi\). Dit betekent dat de formule \(\phi_1\land\ldots \phi_n\rightarrow \psi\) een tautologie is.
Maar deze aanpak zegt weinig over hoe we van een aantal uitgangspunten tot een conclusie komen via een redenering. Met andere woorden: we hebben nog behoefte aan het bewijzen of afleiden van een conclusie op basis van geaccepteerde redeneerstappen. Dit is een syntactische kijk op de geldigheid van een conclusie gebaseerd op afleidingen die starten bij een aantal uitgangspunten. De formule \(\psi\) is nu een conclusie die via een redenering met geaccepteerde redeneerstappen volgt uit een afleiding startend met formules \(\phi_1, \ldots \phi_n \). We noteren dit als \(\phi_1, \ldots \phi_n\vdash \psi\). We zeggen ook wel dat \(\psi\) afleidbaar is uit de formules \(\phi_1, \ldots \phi_n \).
De volgende stelling zegt dat bovenstaande zo verschillend geaarde benaderingen van geldigheid van een gevolgtrekking prima overeenstemmen.
Correctheid en volledigheidsstelling Als \(\Sigma\) een formuleverzameling en \(\psi\) een formule, dan geldt: \[\Sigma\vDash \phi\text{ dan en slechts dan als }\Sigma\vdash \psi\]
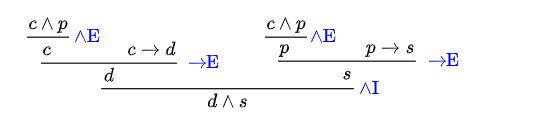
Laten we een concreet voorbeeld gebruiken om een afleiding van een conclusie te illustreren.
We gaan uit van de volgende informatie:
- Claudia programmeert in C++ en Petra programmeert in Python.
- Als Claudia programmeert in C++, dan is de docent blij.
- Als Petra programmeert in Python, dan is de student-assistent blij.
Deze premissen kunnen tot verschillende deelconclusies leiden en deze deelconclusies kunnen samen met de premissen weer tot andere deelconclusies leiden of uitmonden in een slotconclusie.
Stap 1: premisse 1 leidt tot 2 deelconclusies; één daarvan is:
1a. Claudia programmeert in C++.
Immers, als Claudia programmeert in C++ en Petra programmeert in Python, dan is het zeker zo dat Claudia programmeert in C++.
Stap 2: premisse 2 en de deelconclusie 1a leiden tot de deelconclusie:
2a. De docent is blij.
Immers, volgens 1a programmeert Claudia in C++, en het tweede premisezegt dat als Claudia programmeert in C++, dan de docent blij is.
Stap 3: premisse 1 leidt tot 2 deelconclusies; één daarvan is hierboven behandeld en daarom bekijken we nu de andere:
1b. Petra programmeert in Python.
Immers, als Claudia programmeert in C++ en Petra programmeert in Python, dan is het zeker zo dat Petra programmeert in Python.
Stap 4: premisse 3 en de deelconclusie 1b leidt tot de deelconclusie:
2b. De student-assistent is blij.
Immers, volgens 2b programmeert Petra in Python, en de tweede premisse zegt dat als Petra programmeert in Python, dan de student-assistent blij is.
Stap 5: de deelconclusies 2a en 2b kunnen gecombineerd worden tot de volgende slotconclusie:
c. De docent is blij en de student-assistent is blij.
We gebruiken de volgende propositievariabelen:
\(c\) voor "Claudia programmeert in C++."
\(p\) voor "Petra programmeert in Python."
\(d\) voor "de docent is blij."
\(s\) voor "de student-assistent is blij."
Dan kunnen we drie uitgangspunten als logische formules opschrijven: \(c\land p\), \(c\rightarrow d\) en \(p\rightarrow s\).
Ook de (deel)conclusies zijn op te schrijven in de vorm van logische formules: \(\bigl(c\land p)\land (c\rightarrow d)\bigr)\rightarrow d\), \(\bigl((c\land p)\land (p\rightarrow s)\bigr)\rightarrow s\) en \(\bigl((c\land p)\land (c\rightarrow d)\land (p\rightarrow s)\bigr)\rightarrow (d\land s)\).
In de semantische aanpak met modellen toon je aan dat de formules van de (deel)conclusies tautologieën zijn.
In de syntactische aanpak met afleidingen laat je zien hoe je formules combineert via geaccepteerde afleidingsregels tot (deel)conclusies. In de rest van deze sectie gaan we de propositionele taal voor afleiding behandelen. Maar we lichten al vast een tipje van de sluiter op.
Uit de formule \(c\land p\) leiden we de formule \(c\) af via de eliminatieregel voor de conjunctie. Op de formule \(c\) en \(c\rightarrow d\) passen we de eliminatieregel voor de implicatie, beter bekend onder de naam Modus Ponens, toe en we krijgen dan de formule \(d\). Zo kunnen we doorgaan tot de eindconclusie.
Er zijn verschillende notatie in omloop om dit proces te beschrijven. Één daarvan is (met de codes voor de gebruikte afleidingsregels in blauw) de volgende boomstructuur:
Een andere notatie, die wij zullen gaan gebruiken, is de zogenaamde Fitch notatie:
\[\begin{array}{r|ll} 1 & c\land p & (\mathrm{P})\\ 2 & c\rightarrow d & (\mathrm{P})\\ 3 & p\rightarrow s & (\mathrm{P})\\ 4 & c & \land\,\mathrm{E}, 1 \\ 5 & d & \rightarrow\!\mathrm{E}, 2, 4\\ 6 & p & \land\,\mathrm{E}, 1\\ 7 & s & \rightarrow\!\mathrm{E}, 3, 6\\ 8 & d \land s & \land\,\mathrm{I}, 5, 7\end{array}\] De Fitch notatie is bij langere afleidingen gemakkelijker te hanteren.
