Propositional Logic: Natural deduction
 Derivations using natural deduction
Derivations using natural deduction
As suggested by the example on the previous theory page, a deduction using natural deduction essentially boils down to applying accepted steps of reasoning to premises and formulas derived during the reasoning process in order to arrive at a final conclusion. Therefore, we first need to establish some agreements about what is accepted or not, and what types of reasoning steps exist.
Agreements In the subject of natural deduction we assume a propositional language that contains the falsum symbol \(\bot\) as a special constant. This symbol is a logical formula that evaluates \(0\) under any valuation. We also ignore the equivalence connective \(\leftrightarrow\): the formula \(\varphi\leftrightarrow\psi\) is seen henceforth as an abbreviation of \((\varphi\rightarrow\psi)\land(\psi\rightarrow\varphi)\).
There are several variants of natural deduction, but we follow Fitch's proof system as described, for example, in the book Logic, Language, and Meaning by LTF Gamut (1991). Here, the elementary steps of reasoning correspond to the meaning of the different logical connectives, where each connective in principle gives rise to the formulation of two rules.
Rules of reasoning in natural deduction In natural deduction we basically have two elementary steps of reasoning, which are related to a connective:
- An introductory rule \((\mathrm{I})\) that indicates when a formula with this connective as its main sign can be drawn as conclusion.
- An elimination rule \((\mathrm{E})\) that indicated what conclusions can be drawn from a formula with this connective as the main sign;
when drawing the conclusion, the connective will disappear, hence the name elimination rule.
An example of the two types of inference rules for the \(\land\) connective are:
- The introduction of the formula \(\varphi\land\psi\) when the formulas \(\varphi\) and \(\psi\) are available (as premise, intermediate hypothesis, or as sub-conclusion.
- The formulas \(\varphi\) and \(\psi\) are both valid consequences of \(\varphi\land\psi\).
Derivation by natural deduction
Proof A proof or a derivation by natural deduction is, in essence, a finite list of sequentially numbered formulas. At the top are the premises followed by hypotheses, i.e. unproven formulas that can be withdrawn later, and formulas that are conclusions of the previous formulas according to accepted steps of reasoning. Below is an example of a derivation skeleton that we will use as notation. Here \(\varphi_1,\ldots, \varphi_m\) are premises, \(\varphi_{m+1},\ldots \varphi_{n-1}\) derived formulas, and the final formula \(\varphi_n\) as final conclusion.
Usually, in each reasoning step on the right-hand side, you indicate which elementary derivation rule has been applied to arrive at the formula; the numbers are then used to refer to the corresponding formulas. We also use annotations such as \((\mathrm{P})\) and \(\mathrm{(H})\) to indicate whether a formula is a premise or a hypothesis. \[\begin{array}{r|ll} 1 & \varphi_1 & (\mathrm{P})\\ 2 & \varphi_2& (\mathrm{P})\\ &\vdots& \\ m & \varphi_{m} & (\mathrm{P}) \\ m+1 & \varphi_{m+1}\\ \vdots & \vdots \\ n-1 & \varphi_{n-1}\\ n & \varphi_n\end{array}\] We write \[\varphi_1,\ldots,\varphi_m\vdash \varphi_n\] to indicate that \(\varphi_n\) can be derived from the premises \(\varphi_1,\ldots,\varphi_m\). We also say: there exists a derivation of \(\varphi_n\) from (the premises) \(\varphi_1,\ldots,\varphi_m\).
Subproof A hypothesis in a derivation often indicates the beginning of a subproof. Such a subproof ends when the assumption is withdrawn (that is, the hypothesis may no longer be used). Subproofs are represented by an additional vertical line. The hypothesis is separated from the other formulas in the subproof by a horizontal line.
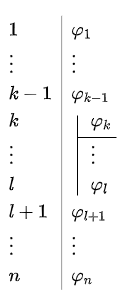
In the above example, the subproof consists of the formulas \(\varphi_k,\ldots \varphi_l\) with hypothesis \(\varphi_k\) and conclusion \(\varphi_l\). Subproofs can themselves have subproofs; you will find a number of examples later on.
There are two conditions in this case. First, formulas from a derivation may be used in subproofs, but not the other way around. In the example above, the formulas \(\varphi_1,\ldots, \varphi_{k-1}\) can be used in both the lines \(k \ldots l\) and \(l+1,\ldots, n\). The formulas \(\varphi_{k},\ldots, \varphi_{l-1}\), on the other hand, cannot be used in the lines \(l+1,\ldots, n\); the conclusion in the subproof ( \(\varphi_l\) ) can be used in an introduction rule. The vertical line shows how long the \(\varphi_k\) hypothesis is active. Second, for a (complete) proof, the result of the derivation must be in the main proof, and not in a subproof. In the example above, the lines of \(1,\ldots l\) do not form a complete proof.
In the rest of this section, we will go through the rules of reasoning one by one. The pen-and-paper assignments about derivations gradually become more complicated because all the rules of reasoning discussed so far can come into play. Also realise that derivationss by natural deduction are not unique; even if your result deviates from the worked-out solution, it does not necessarily mean that it is wrong.


