Propositielogica: Natuurlijke deductie
 Afleidingen via natuurlijke deductie
Afleidingen via natuurlijke deductie
Het voorbeeld in de vorige theoriepagina suggereert het al: een afleiding met natuurlijke deductie komt in principe neer op het toepassen van geaccepteerde redeneerstappen op premissen en tijdens de redenering afgeleide formules om zo te komen tot een slotconclusie. We moeten dus eerst wat afspraken maken wat wel of niet geaccepteerd wordt en wat voor soort redeneerstappen er bestaan.
Afspraken Bij het onderwerp natuurlijke deductie gaan we uit van een propositionele taal die als speciale constante het falsum symbool \(\bot\) bevat. Dit symbool is een logische formule die onder elke waardering \(0\) oplevert. Verder negeren we het equivalentie connectief \(\leftrightarrow\): de formule \(\varphi\leftrightarrow\psi\) wordt hier gezien als afkorting van \((\varphi\rightarrow\psi)\land(\psi\rightarrow\varphi)\).
Er zijn verschillende varianten voor natuurlijke deductie in omloop, maar wij volgen het bewijssysteem van Fitch zoals bijvoorbeeld beschreven in het boek Logic, Language, and Meaning van L.T.F Gamut (1991). Hierin corresponderen de elementaire redeneerstappen met de betekenis van de verschillende logische connectieven, waarbij iedere connectief in principe aanleiding geeft tot het formuleren van twee regels.
Redeneerregels in natuurlijke deductie In natuurlijke deductie hebben we in principe twee elementaire redeneerstappen, die gerelateerd zijn aan een connectief:
- Een introductieregel \((\mathrm{I})\) die aangeeft wanneer tot een formule met het bewuste connectief als hoofdteken kan worden geconcludeerd.
- Een eliminatieregel \((\mathrm{E})\) die aangeeft hoe een formule met dit connectief als hoofdteken kan worden gebruikt;
bij toepassing van de bijbehorende gebruiksregel zal het connectief verdwijnen, vandaar de naam eliminatieregel.
Een voorbeeld van de twee soorten afleidingsregels bij het \(\land\) connectief zijn:
- De introductie van de formule \(\varphi\land\psi\) wanneer de formules \(\varphi\) en \(\psi\) beschikbaar zijn (als premisse, tussentijdse hypothese, of als deelconclusie.
- De formules \(\varphi\) en \(\psi\) zijn allebei een geldige gevolgtrekking uit \(\varphi\land\psi\).
Afleiding met natuurlijke deductie
Bewijs Een bewijs of een afleiding via natuurlijke deductie is in beginsel een eindige lijst van onder elkaar staande genummerde formules. Bovenaan staan de premissen en daaronder hypotheses, d.w.z onbewezen formules die later ingetrokken kunnen worden, en formules die een gevolgtrekking van de vorige formules zijn volgens geaccepteerde redeneerstappen. Hieronder staat een voorbeeld van een geraamte van een afleiding dat we als notatie gaan gebruiken. Hierin zijn \(\varphi_1,\ldots, \varphi_m\) premissen, \(\varphi_{m+1},\ldots \varphi_{n-1}\) afgeleide formules en de laatste formule \(\varphi_n\) als eindconclusie.
Meestal geef je in elke redeneerstap aan de rechterkant nog aan welke elementaire afleidingsregel toegepast is om tot de formule te komen; hierbij worden de nummers dan gebruikt om naar de corresponderende formules te verwijzen. Ook gebruiken we annotaties zoals \((\mathrm{P})\) en \(\mathrm{(H})\) om aan te geven of een formule een premisse dan wel een hypothese is. \[\begin{array}{r|ll} 1 & \varphi_1 & (\mathrm{P})\\ 2 & \varphi_2& (\mathrm{P})\\ &\vdots& \\ m & \varphi_{m} & (\mathrm{P}) \\ m+1 & \varphi_{m+1}\\ \vdots & \vdots \\ n-1 & \varphi_{n-1}\\ n & \varphi_n\end{array}\] We noteren \[\varphi_1,\ldots,\varphi_m\vdash \varphi_n\] om aan te geven dat \(\varphi_n\) afleidbaar is uit de premissen \(\varphi_1,\ldots,\varphi_m\). We zeggen ook: er bestaat een afleiding van \(\varphi_n\) uit (de premissen) \(\varphi_1,\ldots,\varphi_m\).
Deelbewijs Een hypothese in een afleiding geeft vaak het begin van een deelbewijs aan. Zo'n deelbewijs eindigt als de aanname wordt ingetrokken (dat betekent dat de hypothese niet langer gebruikt mag worden). Deelbewijzen worden weergeven met behulp van een extra verticale lijn, De hypothese wordt gescheiden van de andere formules in het deelbewijs door een horizontale lijn.
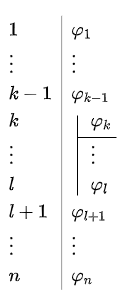
In het bovenstaande voorbeeld bestaat het deelbewijs uit de formules \(\varphi_k,\ldots \varphi_l\) met hypothese \(\varphi_k\) en conclusie \(\varphi_l\). Deelbewijzen kunnen zelf ook weer deelbewijzen hebben; verderop vindt u een
aantal voorbeelden.
Er zijn wel twee voorwaarden in dit geval. Ten eerste mogen formules uit een afleiding worden gebruikt in deelbewijzen, maar niet andersom. In het bovenstaande voorbeeld zijn de formules \(\varphi_1,\ldots, \varphi_{k-1}\) zowel te gebruiken in de regels \(k \ldots l\) als in de regels \(l+1,\ldots, n\). De formules \(\varphi_{k},\ldots, \varphi_{l-1}\) zijn daarentegen niet te gebruiken in de regels \(l+1,\ldots, n\); de conclusie in het deelbewijs (\(\varphi_l\)) is wel te gebruiken bij een introductieregel. Aan de verticale streep valt te zien hoelang de hypothese \(\varphi_k\) actief is. Ten tweede moet voor een (volledig) bewijs het resultaat van de afleiding in het hoofdbewijs staan, en niet in een deelbewijs. In het voorbeeld hierboven vormen de regels \(1,\ldots l\) geen compleet bewijs.
In de rest van deze sectie lopen we de redeneerregels één voor één langs. De pen-en-papier opdrachten over afleidingen worden gaandeweg ingewikkelder doordat alle tot dan toe besproken redeneerregels een rol mogen spelen. Realiseer je ook dat afleidingen via natuurlijke deductie niet uniek zijn; ook al wijkt jouw resultaat af van de voorbeelduitwerking, dan hoeft deze niet per se fout te wezen.


