Implication reasoning rules and the repetition rule

Propositional Logic: Natural deduction

Implication reasoning rules and the repetition rule

Introduction rule for implication The introduction rule \(\rightarrow\!\mathrm{I}\) for the connective \(\rightarrow\) is as follows:

implicatie-introductie

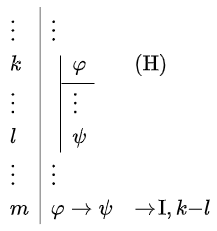
This means that if we assume the hypothesis \(\varphi\), then the formula \(\varphi\rightarrow \psi\) can be derived in a subproof. The formulas in line \(k\) through \(l\) are not available outside this subproof, but in line \(l+1\) we mention them only to indicate the scope of the subproof. Strictly speaking, we can do without line numbers because the vertical line already indicates when the subproof ends and the conclusion \(\varphi\rightarrow \psi\) is drawn.

Although it is not mandatory to apply the introduction rule immediately at the end of the subproof, this is the most natural place.

The repetition rule The repetition rule, denoted by the letter R for repetition, is as follows: \[\begin{array}{l|ll}\vdots & \vdots & \\ k & \varphi & \\ \vdots & \vdots \\ l & \varphi & \mathrm{R}, k\end{array}\] With this, in a later stage of a derivation, you can repeat any formula that is not a hypothesis that has already been withdrawn or depends on such a hypothesis. In other words, formulas can be repeated from a main proof to a subproof, but not the other way around.

Examples

\(\vdash (p\land q)\rightarrow q\)	\(\vdash p\rightarrow (q\rightarrow p)\)	\((p\land q)\rightarrow r \vdash (q\land p)\rightarrow r\)

\(\phantom{x}\)

Explanation of example 3 Because the third example already contains the elimination rule for implication and it may not be very clear how you arrive at this derivation, we will work out the details below.

We start the derivation with the premise \((p\land q)\rightarrow r\).
From this we want to derive the formula \((q\land p)\rightarrow r\). This is an implication. We choose the left member \(q\land p\) in this as a hypothesis in a subproof to derive the sub-conclusion \(r\).
From the \(q\land p\) hypothesis, we can eliminate any propositional variable.
The right-hand side of \((q\land p)\rightarrow r\), the propositional variable \(r\), is extracted from the premise via the \(\rightarrow\!\mathrm{E}\) elimination rule.
Finally, we use the introduction rule \(\rightarrow\!\mathrm{I}\) to construct the desired implication. After this, only lines 1 and 7 would be available if the diversion were to continue.

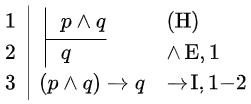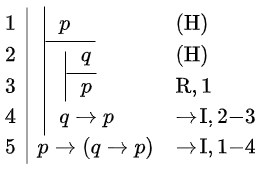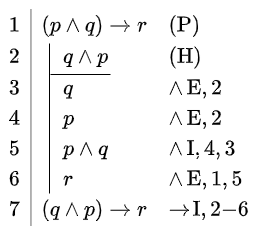Elimination rule for implication The elimination rule \(\rightarrow\!\mathrm{E}\) for the connective \(\rightarrow\) is as follows:

\[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi\rightarrow\psi & \\ \vdots & \vdots & \\ l &\varphi & \\ \vdots & \vdots & \\ m & \psi & \rightarrow\!\mathrm{E}, k, l \end{array}\]

\[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi & \\ \vdots & \vdots & \\ l &\varphi\rightarrow \psi & \\ \vdots & \vdots & \\ m & \psi & \rightarrow\!\mathrm{E}, k, l \end{array}\]

The elimination rule is also known as Modus Ponens: From \(\varphi\rightarrow \phi\) it follows, if \(\varphi\) is available, that the conclusion \(\psi\) can be drawn.

The order in which the formulas \(\varphi\rightarrow \psi\) and \(\varphi\) are available in the derivation does not matter.

Examples

\(p\rightarrow q, p\vdash q\)	\( p\land r, r\rightarrow q\vdash p\land q\)	\(\bigl(p\rightarrow (q\rightarrow r)\bigr), p\rightarrow q, p \vdash r\)
\[\begin{array}{l\|ll} 1 & p\land q & (\mathrm{P})\\ 2 & p & (\mathrm{P})\\ 3 & q & \rightarrow\!\mathrm{E}, 1, 2\end{array}\]	\[\begin{array}{l\|ll} 1 & p\land r & (\mathrm{P})\\ 2 & r\rightarrow q & (\mathrm{P})\\ 3 & p & \land\,\mathrm{E}, 1\\ 4 & r & \land\,\mathrm{E}, 1\\ 5 & q& \rightarrow\!\mathrm{E}, 2, 4\\ 6 & p\land q & \land\,\mathrm{I}, 3,5\\ \end{array}\]	\[\begin{array}{l\|ll} 1 &p\rightarrow (q\rightarrow r) & (\mathrm{P})\\ 2 & p\rightarrow q & (\mathrm{P})\\ 3 & p & (\mathrm{P})\\ 4 & q & \rightarrow\!\mathrm{E}, 2,3\\ 5 & q\rightarrow r & \rightarrow\!\mathrm{E}, 1,3\\ 6 & r & \rightarrow\!\mathrm{E}, 4,5 \end{array}\]