Implicatie-redeneerregels en de herhalingsregel

Propositielogica: Natuurlijke deductie

Implicatie-redeneerregels en de herhalingsregel

Introductieregel voor implicatie De introductieregel \(\rightarrow\!\mathrm{I}\) voor het connectief \(\rightarrow\) is:

implicatie-introductie

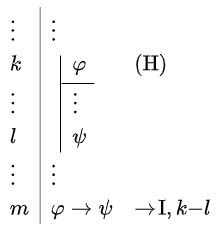
Hier staat dus dat als we de hypothese \(\varphi\) stellen dan de formule \(\varphi\rightarrow \psi\) in een deelbewijs afgeleid kan worden. De formules in regel \(k\) t/m \(l\) zijn niet beschikbaar buiten dit deelbewijs, maar in de regel \(l+1\) vermelden we ze enkel nog om het domein van het deelbewijs aan te geven; strikt genomen kunnen we ook zonder regelnummers want de verticale lijn geeft al aan wanneer het deelbewijs stopt en de conclusie \(\varphi\rightarrow \psi\) getrokken wordt.

Ofschoon het niet verplicht is om de introductieregel onmiddellijk aan het einde van het deelbewijs toe te passen is dit wel de meest natuurlijke plek.

De herhalingsregel De herhaingsregel, aangeduid met de letter R van repetitie, is: \[\begin{array}{l|ll}\vdots & \vdots & \\ k & \varphi & \\ \vdots & \vdots \\ l & \varphi & \mathrm{R}, k\end{array}\] Je kunt hiermee in een later stadium van een afleiding elke formule herhalen die geen hypothese is die al ingetrokken is of van zo'h hypothese afhangt. Met andere woorden: formules mogen wel herhaald worden van een hoofdbewijs naar een deelbewijs, maar niet andersom.

Voorbeelden

\(\vdash (p\land q)\rightarrow q\)	\(\vdash p\rightarrow (q\rightarrow p)\)	\((p\land q)\rightarrow r \vdash (q\land p)\rightarrow r\)

\(\phantom{x}\)

Toelichting bij voorbeeld 3 Omdat het derde voorbeeld ook al de eliminatieregel voor implicatie bevat en het misschien ook niet zo helder is hoe je aan deze afleiding komt werken we de details hieronder uit.

We beginnen de afleiding met de premisse \((p\land q)\rightarrow r\).
Hieruit willen we de formule \((q\land p)\rightarrow r\) afleiden . Dit is een impliciatie. Het linkerlid \(q\land p\) hierin kiezen we als hypothese in een deelbewijs om de deelconclusie \(r\) af te leiden.
Uit de hypothese \(q\land p\) kunnen we elke propostieivariabele elimineren.
Het rechterlid van \((q\land p)\rightarrow r\), de propositievariabele \(r\), halen we via de eliminatieregel \(\rightarrow\!\mathrm{E}\) uit de premisse.
Tot slot gebruiken we de introductieregel \(\rightarrow\!\mathrm{I}\) om de gewenste implicatie te construeren. Hierna zijn alleen regels 1 en 7 nog beschikbaar als de afleiding verder zou gaan.

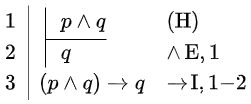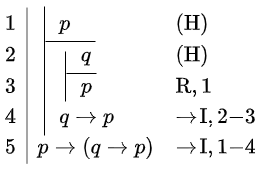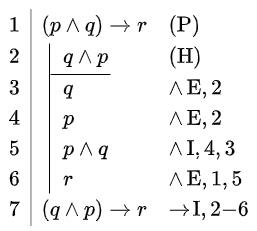Eliminatieregel voor implicatie De eliminatieregel \(\rightarrow\!\mathrm{E}\) voor het connectief \(\rightarrow\) is:

\[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi\rightarrow\psi & \\ \vdots & \vdots & \\ l &\varphi & \\ \vdots & \vdots & \\ m & \psi & \rightarrow\!\mathrm{E}, k, l \end{array}\]

\[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi & \\ \vdots & \vdots & \\ l &\varphi\rightarrow \psi & \\ \vdots & \vdots & \\ m & \psi & \rightarrow\!\mathrm{E}, k, l \end{array}\]

De eliminatieregel staat ook bekend als Modus Ponens: Uit \(\varphi\rightarrow \phi\) volgt bij beschikbaarheid van \(\varphi\) dat de conclusie \(\psi\) getrokken kan worden.

De volgorde waarin de formules \(\varphi\rightarrow \psi\) en \(\varphi\) beschikbaar zijn in de afleiding doet er niet toe.

Voorbeelden

\(p\rightarrow q, p\vdash q\)	\( p\land r, r\rightarrow q\vdash p\land q\)	\(\bigl(p\rightarrow (q\rightarrow r)\bigr), p\rightarrow q, p \vdash r\)
\[\begin{array}{l\|ll} 1 & p\land q & (\mathrm{P})\\ 2 & p & (\mathrm{P})\\ 3 & q & \rightarrow\!\mathrm{E}, 1, 2\end{array}\]	\[\begin{array}{l\|ll} 1 & p\land r & (\mathrm{P})\\ 2 & r\rightarrow q & (\mathrm{P})\\ 3 & p & \land\,\mathrm{E}, 1\\ 4 & r & \land\,\mathrm{E}, 1\\ 5 & q& \rightarrow\!\mathrm{E}, 2, 4\\ 6 & p\land q & \land\,\mathrm{I}, 3,5\\ \end{array}\]	\[\begin{array}{l\|ll} 1 &p\rightarrow (q\rightarrow r) & (\mathrm{P})\\ 2 & p\rightarrow q & (\mathrm{P})\\ 3 & p & (\mathrm{P})\\ 4 & q & \rightarrow\!\mathrm{E}, 2,3\\ 5 & q\rightarrow r & \rightarrow\!\mathrm{E}, 1,3\\ 6 & r & \rightarrow\!\mathrm{E}, 4,5 \end{array}\]