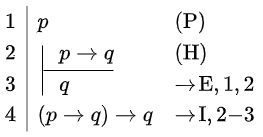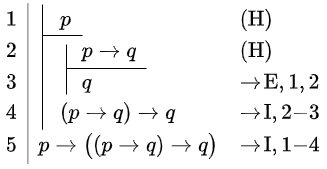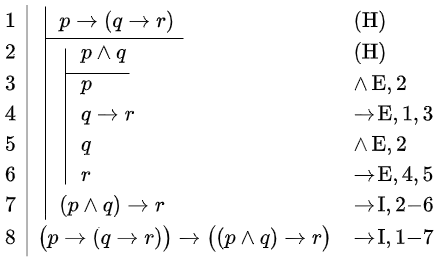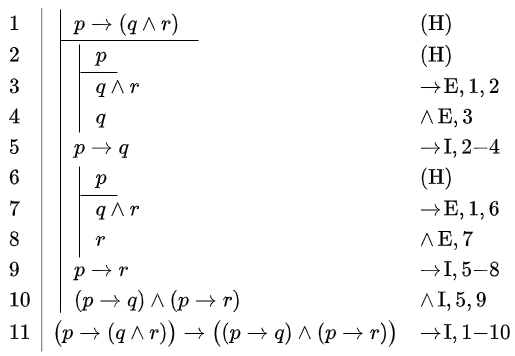Propositional Logic: Natural deduction
Implication reasoning rules: pencil-and-paper exercises (4 exercises)
First, attempt each exercise on your own, and then compare your answer with the worked-out solution.
Exercise 1 Show that \(p\vdash (p\rightarrow q) \rightarrow q\).
Worked-out solution 
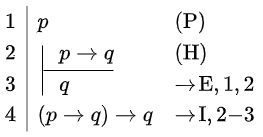
The formula you need to derive is the implication \(p\vdash (p\rightarrow q) \rightarrow q\). Therefore, after the premise in line 1, you should place the hypothesis \(p\rightarrow q\) in line 2. The first two lines enable the application of the Modus Ponens reasoning step in line 3. The subproof in lines 2 and 3 then yields the implication formula in line 4.
Exercise 2 Show that \(\vdash p\rightarrow\bigl((p\rightarrow q) \rightarrow q\bigr)\).
Worked-out solution 
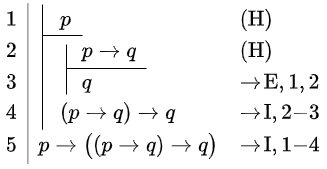
The formula you need to derive is the implication \( p\rightarrow\bigl((p\rightarrow q) \rightarrow q\bigr)\). That is why you should immediately place the hypothesis \(p\) in line 1. The hypothesis in the first line and the hypothesis \(p\rightarrow q\) in the second line enablethe application of the Modus Ponens reasoning step in line 3, resulting in the implication in line 4. The subproof in lines 1 through 4 then yields the implication formula on line 5.
Exercise 3 Show that \(\vdash \bigl(p\rightarrow(q\rightarrow r)\bigr)\rightarrow \bigl((p\land q)\rightarrow r\bigr)\).
Worked-out solution 
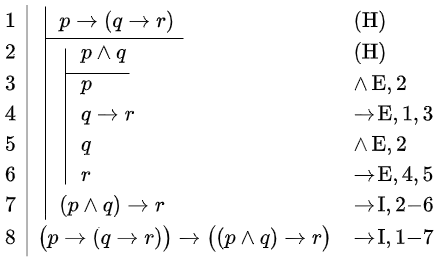
The formula you need to derive is the \( \bigl(p\rightarrow(q\rightarrow r)\bigr)\rightarrow \bigl((p\land q)\rightarrow r\bigr)\) implication. Therefore, you should immediately set the hypothesis \(p\rightarrow(q\rightarrow r)\). Since the right-hand side of the implication \(\bigl(p\rightarrow(p\rightarrow q)\bigr)\rightarrow \bigl((p\land q)\rightarrow r\bigr)\) is another implication, namely \((p\land q)\rightarrow r\), you need to set another hypothesis in the second rule, which is \(p\land q\). In line 3 we apply a \(\land\) elimination rule to obtain the propositional variable \(p\) because then the hypothesis in the first line and the proposition variable \(p\) in the third line allow us to apply the Modus Ponens reasoning step in line 4. In line 5 we again apply a \(\land\) elimination rule to the second hypothesis, but this time to obtain the propositional variable \(q\). Once again, we have the opportunity to apply the Modus Ponens reasoning step to lines 4 and 5. This yields the propositional variable \(r\) in line 6. We need it to apply the introduction rule for implication for the subproof of lines 2 through 6. The sub-conclusion in line 7 is \((p\land q)\rightarrow r\). Finally, we apply the introduction rule of implication once more to derive the final conclusion.
Exercise 4 Show that \(\vdash \bigl(p\rightarrow (q\land r)\bigr)\rightarrow \bigl((p\rightarrow q) \land (p\rightarrow r)\bigr)\).
Worked-out solution 
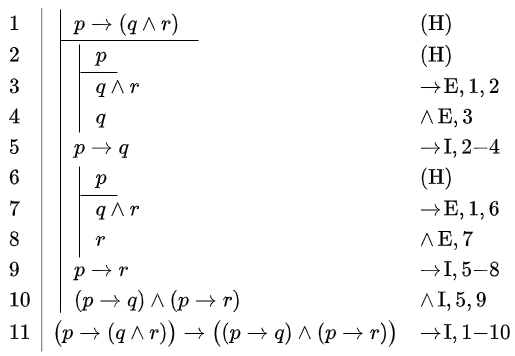
The formula you need to derive is the implication \( \bigl(p\rightarrow (q\land r)\bigr)\rightarrow \bigl((p\rightarrow q) \land (p\rightarrow r)\bigr)\). Therefore, you should immediately set the hypothesis \(p\rightarrow (p\rightarrow (q\land r))\). The right-hand side of the implication \( (p\rightarrow q) \land (p\rightarrow r)\) consists of two implications, each of which is derived in a subproof via the Modus Ponens reasoning rule.
