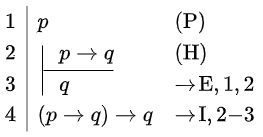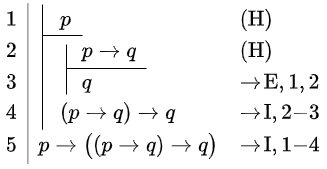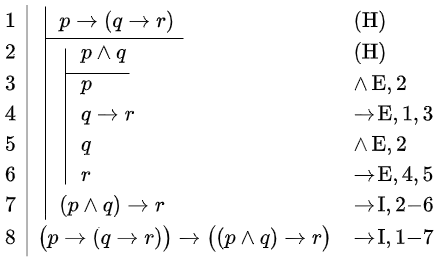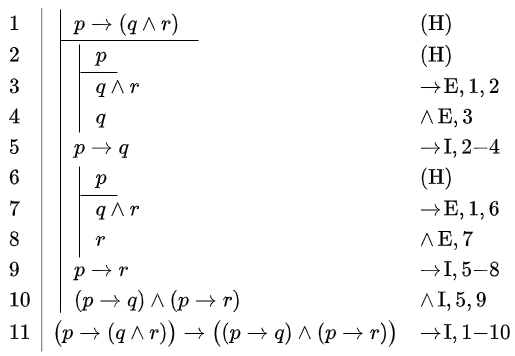Propositielogica: Natuurlijke deductie
Implicatie-redeneerregels: pen-en-papier opdrachten (4 opdrachten)
Maak eerst elke opdracht zelf en vergelijk daarna pas jouw antwoord met de uitwerking.
Opdracht 1 Toon aan dat \(p\vdash (p\rightarrow q) \rightarrow q\).
Uitwerking 
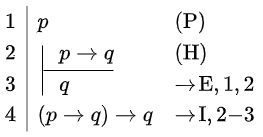
De formule die je moet afleiden is de implicatie \(p\vdash (p\rightarrow q) \rightarrow q\). Daarom moet je na de premisse in regel 1 in regel 2 de hypothese \(p\rightarrow q\) plaatsen. De eerste twee regels maken de toepassing van de redeneerstap Modus Ponens in regel 3 mogelijk. Het deelbewijs in regels 2 en 3 levert dan de implicatie formule in regel 4 op.
Opdracht 2 Toon aan dat \(\vdash p\rightarrow\bigl((p\rightarrow q) \rightarrow q\bigr)\).
Uitwerking 
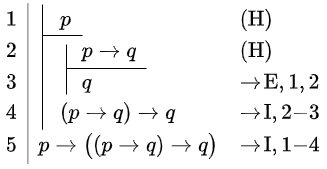
De formule die je moet afleiden is de implicatie \( p\rightarrow\bigl((p\rightarrow q) \rightarrow q\bigr)\). Daarom moet je meteen in regel 1 de hypothese \(p\) stellen. De hypothese in de eerste regel en de hypothese \(p\rightarrow q\) in de tweede regel maken de toepassing van de redeneerstap Modus Ponens in regel 3 mogelijk en levert de implicatie in regel 4 op. Het deelbewijs in regels 1 t/m 4 levert dan de implicatie formule op regel 5.
Opdracht 3 Toon aan dat \(\vdash \bigl(p\rightarrow(q\rightarrow r)\bigr)\rightarrow \bigl((p\land q)\rightarrow r\bigr)\).
Uitwerking 
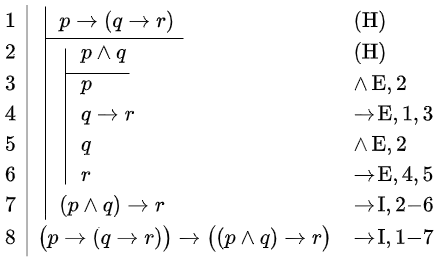
De formule die je moet afleiden is de implicatie \( \bigl(p\rightarrow(q\rightarrow r)\bigr)\rightarrow \bigl((p\land q)\rightarrow r\bigr)\). Daarom moet je meteen de hypothese \(p\rightarrow(q\rightarrow r)\) stellen. Omdat de rechterkant van de implicatie \(\bigl(p\rightarrow(p\rightarrow q)\bigr)\rightarrow \bigl((p\land q)\rightarrow r\bigr)\) ook weer een implicatie is, namelijk \((p\land q)\rightarrow r\), moet je in de tweede regel weer een hypothese stellen en wel \(p\land q\). In regel 3 passen we hierop een \(\land\) eliminatieregel toe om de proposititevariabele \(p\) te verkrijgen want dan maken de hypothese in de eerste regel en de propositievariable \(p\) in de derde regel de toepassing van de redeneerstap Modus Ponens in regel 4 mogelijk. In regel 5 passen we weer op de tweede hypothese een \(\land\) eliminatieregel toe, maar nu om de proposititevariabele \(q\) te verkrijgen. Opnieuw is de redeneerstap Modus Ponens mogelijk met regels 4 en 5. Dit levert in regel 6 de propositievariabele \(r\) op. Die hebben we nodig om de introductieregel voor implicatie te kunnen toepassen voor het deelbewijs van regel 2 t/m 6. De deelconclusie in regel 7 is \((p\land q)\rightarrow r\). Tenslotte passen we de introductieregel voor implicatie nogmaals toe om de eindconclusie af te leiden.
Opdracht 4 Toon aan dat \(\vdash \bigl(p\rightarrow (q\land r)\bigr)\rightarrow \bigl((p\rightarrow q) \land (p\rightarrow r)\bigr)\).
Uitwerking 
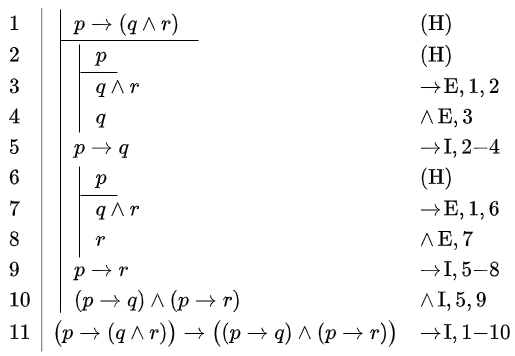
De formule die je moet afleiden is de implicatie \( \bigl(p\rightarrow (q\land r)\bigr)\rightarrow \bigl((p\rightarrow q) \land (p\rightarrow r)\bigr)\). Daarom moet je meteen de hypothese \(p\rightarrow (p\rightarrow (q\land r))\) stellen. De rechterkant van de implicatie \( (p\rightarrow q) \land (p\rightarrow r)\) bestaat uit twee implicaties die ieder voor zich in een deelbewijs via de redeneerregel Modus Ponens afgeleid worden.
