Propositional Logic: Natural deduction
Disjunction reasoning rules
Introduction rule for disjunction The introduction rule \(\lor\,\mathrm{I}\) for the connective \(\lor\) is as follows:
| \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi & \\ \vdots & \vdots & \\ l & \varphi\lor\psi & \lor\,\mathrm{I}, k \end{array}\] | \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\psi & \\ \vdots & \vdots & \\ l & \varphi\lor\psi & \lor\,\mathrm{I}, k \end{array}\] |
Examples
| \(p \vdash p\lor q\) | \(\vdash p\rightarrow (p\lor q)\) | \(p, q, r\vdash (p\lor q)\lor r\) |
| \[\begin{array}{l|ll} 1 & p & (\mathrm{P}) \\ 2 & p \lor q & \lor\,\mathrm{I}, 1 \end{array}\] |  |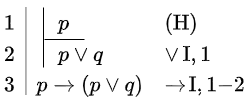
\[\begin{array}{l|ll} 1 & p & (\mathrm{P}) \\ 2 & q & (\mathrm{P}) \\ 3 & r & (\mathrm{P}) \\ 4 & p\lor q & \lor\,\mathrm{I}, 1 \\ 5& (p\lor q)\lor r & \lor\,\mathrm{I}, 4\end{array}\] |
Elimination rule for conjunction The elimination rule \(\lor\,\mathrm{E}\) for the connective \(\lor\) can be applied in two ways; it is a matter of taste whether you want to use introductions of the implications or not (we prefer this because the two implication formulas separate the subproofs better, but we still show two examples of the other notation below):
 |
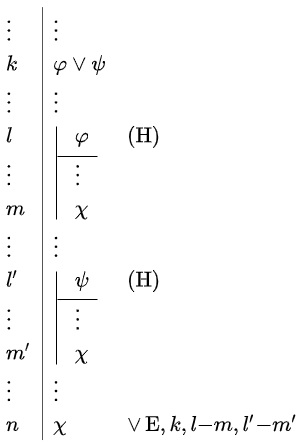\[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi\lor\psi & \\ \vdots & \vdots & \\ l & \varphi\rightarrow \chi & \\ \vdots & \vdots & \\ m & \psi\rightarrow \chi & \\ \vdots & \vdots & \\ n & \chi & \lor\,\mathrm{E}, k,l,m\end{array}\] |
Examples
| \(p\lor q, q\rightarrow r\vdash p\lor r\) | \(p\land q\vdash p\lor r\) | \(p\lor(q\land r)\vdash p\lor q\) |
 |
 |
 |
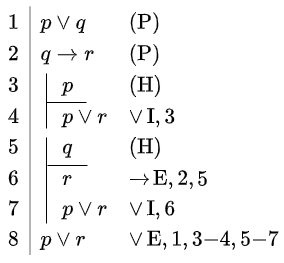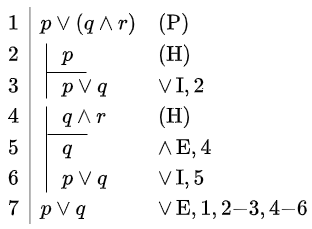Unlock full access
