Propositielogica: Natuurlijke deductie
Disjunctie-redeneerregels
Introductieregel voor disjunctie De introductieregel \(\lor\,\mathrm{I}\) voor het connectief \(\lor\):
| \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi & \\ \vdots & \vdots & \\ l & \varphi\lor\psi & \lor\,\mathrm{I}, k \end{array}\] | \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\psi & \\ \vdots & \vdots & \\ l & \varphi\lor\psi & \lor\,\mathrm{I}, k \end{array}\] |
Voorbeelden
| \(p \vdash p\lor q\) | \(\vdash p\rightarrow (p\lor q)\) | \(p, q, r\vdash (p\lor q)\lor r\) |
| \[\begin{array}{l|ll} 1 & p & (\mathrm{P}) \\ 2 & p \lor q & \lor\,\mathrm{I}, 1 \end{array}\] |  |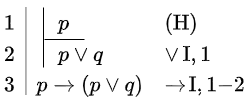
\[\begin{array}{l|ll} 1 & p & (\mathrm{P}) \\ 2 & q & (\mathrm{P}) \\ 3 & r & (\mathrm{P}) \\ 4 & p\lor q & \lor\,\mathrm{I}, 1 \\ 5& (p\lor q)\lor r & \lor\,\mathrm{I}, 4\end{array}\] |
Eliminatieregel voor conjunctie De eliminatieregel \(\lor\,\mathrm{E}\) voor het connectief \(\lor\) is op twee manieren op te schrijven; het is een kwestie van smaak of je introducties van de implicaties wilt toepassen of niet (wij prefereren dit wel omdat de twee implicatie-formules de deelbewijzen beter uit elkaar houdt, maar laten hieronder nog wel twee voorbeelden van de andere notatie zien):
 |
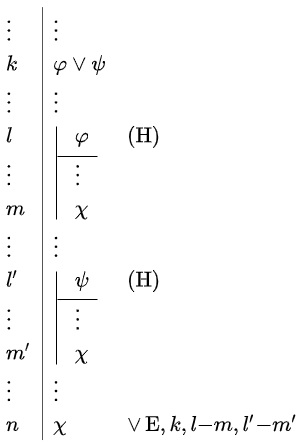\[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi\lor\psi & \\ \vdots & \vdots & \\ l & \varphi\rightarrow \chi & \\ \vdots & \vdots & \\ m & \psi\rightarrow \chi & \\ \vdots & \vdots & \\ n & \chi & \lor\,\mathrm{E}, k,l,m\end{array}\] |
Voorbeelden
| \(p\lor q, q\rightarrow r\vdash p\lor r\) | \(p\land q\vdash p\lor r\) | \(p\lor(q\land r)\vdash p\lor q\) |
 |
 |
 |
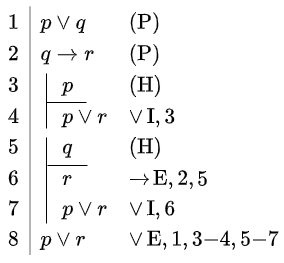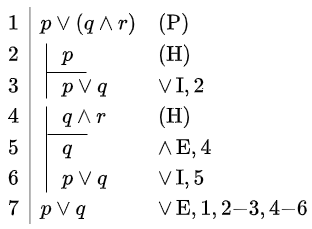Ontgrendel volledige toegang
