Propositional Logic: Natural deduction
 Negation reasoning rules
Negation reasoning rules
In the negation reasoning rules we use the falsum \(\bot\) symbol for an always false proposition.
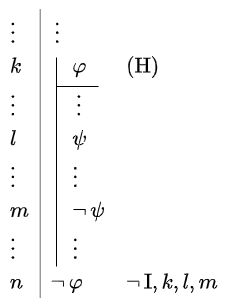
Introduction rule for negation The introduction rule \(\neg\,\mathrm{I}\) for the connective \(\neg\) is as follows:
This means that if we set the hypothesis \(\varphi\) then we can derive in the negation \(\neg\,\varphi\) within a subproof can be derived because the subproof leads to the falsum \(\bot\) in it. The formulas in lines \(k\) through \(l\) are not available outside this subproof, but in line \(l+1\) we only list them to indicate the scope of the subproof. Strictly speaking, we can do without rule numbers because the vertical line already indicates when the subproof ends and the conclusion \(\neg\,\varphi\) is drawn.
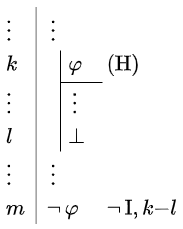
Elimination rule for negation The elimination rule \(\neg\,\mathrm{E}\) for the connective \(\neg\) can be applied in two ways (as long as we do not yet have a rule for double negation). In both cases, the conclusion is equivalent to the falsum \(\bot\):
| \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi & \\ \vdots & \vdots & \\ l & \neg\,\varphi &\\ \vdots & \vdots & \\ m & \bot & \neg\,\mathrm{E}, k,l \end{array}\] | \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\neg\,\varphi & \\ \vdots & \vdots & \\ l & \varphi &\\ \vdots & \vdots & \\ m & \bot & \neg\,\mathrm{E}, k,l \end{array}\] |
Examples
| \(\vdash \neg(p\land \neg\,p)\) | \(p\vdash \neg\neg\,p\) | \((p\rightarrow q)\vdash (\neg \, q\rightarrow \neg\, p)\) |
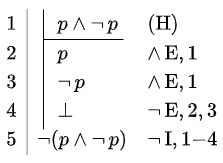 |
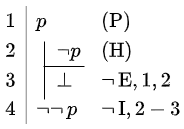 |
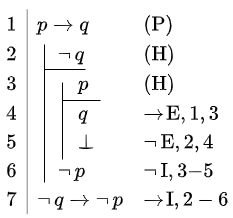 |