Propositielogica: Natuurlijke deductie
 Negatie-redeneerregels
Negatie-redeneerregels
Bij de redeneerregels voor negatie gebruiken we het falsum \(\bot\) symbool voor een altijd onware propositie.
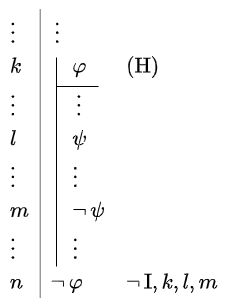
Introductieregel voor negatie De introductieregel \(\neg\,\mathrm{I}\) voor het connectief \(\neg\):
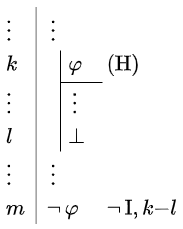
Hier staat dus dat als we de hypothese \(\varphi\) stellen dan de negatie \(\neg\,\varphi\) in een deelbewijs afgeleid kan worden doordat het deelbewijs leidt tot het falsum \(\bot\) hierin. De formules in regel \(k\) t/m \(l\) zijn niet beschikbaar buiten dit deelbewijs, maar in de regel \(l+1\) vermelden we ze enkel nog om het domein van het deelbewijs aan te geven; strikt genomen kunnen we ook zonder regelnummers want de verticale lijn geeft al aan wanneer het deelbewijs stopt en de conclusie \(\neg\,\varphi\) is.
Eliminatieregel voor negatie De eliminatieregel \(\neg\,\mathrm{E}\) voor het connectief \(\neg\) is op twee manieren toe te passen (zolang we nog geen regel voor de dubbele negatie hebben). In beide gevallen is de conclusie gelijk aan het falsum \(\bot\):
| \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\varphi & \\ \vdots & \vdots & \\ l & \neg\,\varphi &\\ \vdots & \vdots & \\ m & \bot & \neg\,\mathrm{E}, k,l \end{array}\] | \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\neg\,\varphi & \\ \vdots & \vdots & \\ l & \varphi &\\ \vdots & \vdots & \\ m & \bot & \neg\,\mathrm{E}, k,l \end{array}\] |
Voorbeelden
| \(\vdash \neg(p\land \neg\,p)\) | \(p\vdash \neg\neg\,p\) | \((p\rightarrow q)\vdash (\neg \, q\rightarrow \neg\, p)\) |
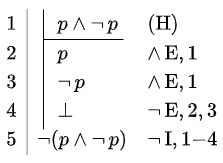 |
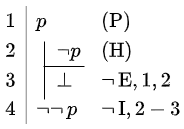 |
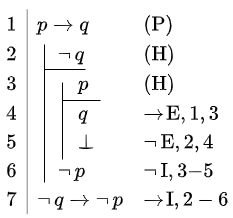 |