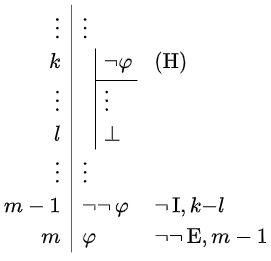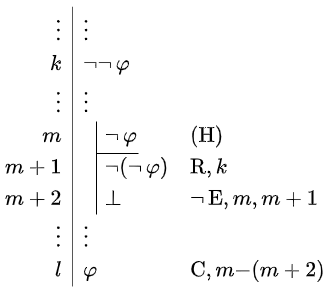Propositional Logic: Natural deduction
Double negation elimination rule
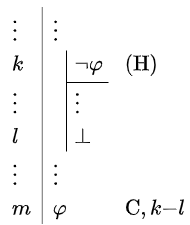
With the rules of reasoning we have dealt with so far, we arrive at a proof system of intuitionistic logic. in which the rule of excluded third \(p \lor \neg\, p\) is not used as a theorem. In classical propositional logic we do want this rule and for that we introduce the double negation elimination rule.
Elimination rule for double negation The elimination rule \(\neg\neg\,\mathrm{E}\) for the double negation is as follows: \[\begin{array}{l|ll} \vdots & \vdots &\\ k &\neg\neg\,\varphi & \\ \vdots & \vdots & \\ l & \varphi& \neg\neg\,\mathrm{E}, k \end{array}\]
Double negation vs proof by contradiction The proof by contradiction can also be found in the literature in the following form of a rule of reasoning:
With the double negation rule we can also derive this reasoning rule from the previous reasoning rules:
Conversely, you can derive the double negation reasoning rule from the above rule for the proof by contradiction:
In short, it doesn't matter to classical propositional logic whether you use within a derivation the double negation reasoning rule or the rule that allows the proof by contradiction.
With the double negation elimination rule we can prove the formula \(p\lor \neg\,p\) without any premises:
