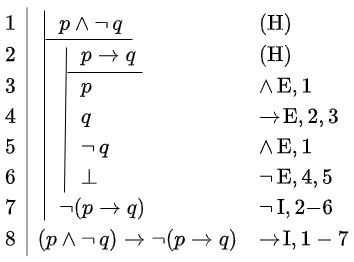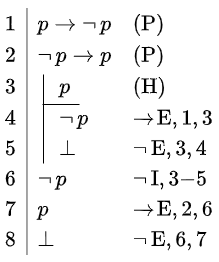Propositional Logic: Natural deduction
Negation reasoning rules: pencil-and-paper exercises (3 exercises)
First, attempt each exercise on your own, and then compare your answer with the worked-out solution.
Exercise 1 Show that \(\vdash (p\land \neg\,q)\rightarrow \neg(p \rightarrow q)\).
Worked-out solution
Esercise 2 Show that \(\vdash \neg(p\lor q)\rightarrow (\neg\, p\land \neg\, q)\).
Worked-out solution
Exercise 3 The liar's paradox is a well-known logical paradox that can be formulated as follows: "This statement is not true". If this proposition is true, then it is not true, and contradicts itself. However, if this statement is not true, then it is not the case that it is not true - after all, that is what is stated - and it is therefore true. The sentence is therefore true if and only if it is not true. In propositional language, the problem is:
Show that \(p\rightarrow \neg\,p, \neg\,p\rightarrow p\vdash\bot\).
Worked-out solution
