We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}=1-2\,t\, y\] Het lijnelementenveld van de bovenstaande differentiaalvergelijking kunnen we plotten door gebruik te maken van grafische elementen zoals lijnen.

xp <- seq(from=0, to=2, length=10)
yp <- seq(from=0, to=2, length=10)

plot(c(0,2),c(0,2), main="lijnelementenveld van y'= 1 - 2ty", ylab = "y", xlab = "t", pch = ".")

for(x in xp){
  for(y in yp){
    u <- 1.0
    v <- 1.0 - 2.0*x*y
    L <- sqrt(u*u+v*v)
    u <- u/L
    v <- v/L
    segments(x-0.05*u,y-0.05*v,x+0.05*u,y+0.05*v, col="blue")
  }
}

Het resultaat is de volgende figuur:

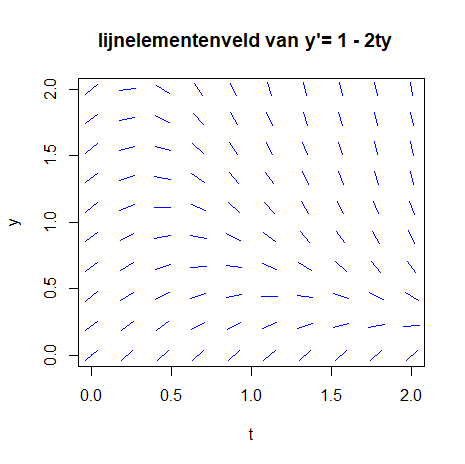De lijnelementen in bovenstaande figuur bevinden zich gecentreerd op een regelmatig rooster. We kunnen dit programma ook zo aanpassen dat er \(2000\) willekeurige coördinaten worden gerandomiseerd op het gebied \(0\le t\le 2, 0\le y\le 2, \). Daarna tekenen we op dezelfde manier als hiervoor de lijnen op deze coördinaten. Hieronder staat een voorbeeld van de R code:

xp <- runif(2000, min=0, max=2)
yp <- runif(2000, min=0, max=2)

plot(c(0,2),c(0,2), main="lijnelementenveld van y'= 1 - 2ty", ylab = "y", xlab = "t", pch = ".")

for(k in 1:2000){
  x <- xp[k]
  y <- yp[k]
  u <- 1.0
  v <- 1.0 - 2.0*x*y
  L <- sqrt(u*u+v*v)
  u <- u/L
  v <- v/L
  segments(x-0.05*u,y-0.05*v,x+0.05*u,y+0.05*v, col="gray")
}

Het resultaat is nu onderstaande figuur:

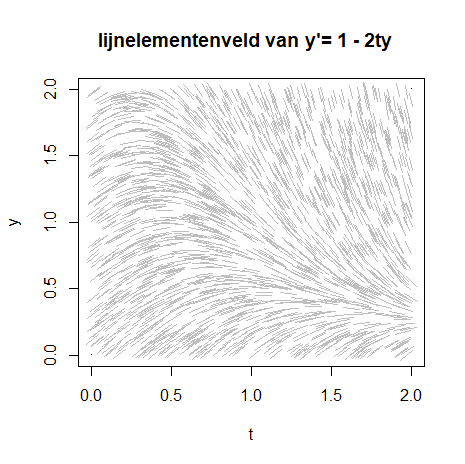Net als ijzervijlsel de veldlijnen van een magnetisch veld zichtbaar maken, zo maakt ook bovenstaand lijnelementnveld de oplossingskrommen zichtbaar.

In dit voorbeeld bekijken we de differentiaalvergelijking \[\frac{\dd y}{\dd t}=\frac{4-2t}{3y^2-5}\] lossen deze op en tekenen een faseportret.

Eerst schrijven we de differentiaalvergelijking in differentiaalvorm, waarbij we gelijk scheiding van variabelen toepassen: \[(3y^2-5)\,\dd y=(4-2t)\,\dd t\] Als we aan beide kanten integreren krijgen we \[\int (3y^2-5)\,\dd y=\int (4-2t)\,\dd t\] Dus: \[y^3 -5y=4t-t^2+C\] voor zekere constante \(C\). Met andere woorden \[F(t,y)=C\] voor \[F(t,y)=y^3-5y+t^2-4t\] We tekenen vervolgens een lijnelementenveld en enkelen integraalkrommen in één diagram. Het laatste aspect betreft het tekenen van contourgrafiek van de functie \[F(t,y)=y^3-5y+t^2-4t\] De volgende R code, waarin gebruik gemaakt wordt van de pakketten ggplot2 en dplyr, levert onderstaand diagram op:

# laad R pakketten
library(dplyr)
library(ggplot2)

# bereid de berekening van het lijnelementenveld voor
tp <- seq(from=-3, to=7, by=0.5)
yp <- seq(from=-4, to=4, by=0.5)

px <- c()
py <- c()
vx <- c()
vy <- c()
for(t in tp){
  for(y in yp){
    u <- 1.0
    v <- (4.0-2.0*t)/(3.0*y^2-5.0)
    L <- sqrt(u*u+v*v)
    u <- u/L
    v <- v/L
    px <- c(px, t-0.15*u)
    py <- c(py, y-0.15*v)
    vx <- c(vx, 0.3*u)
    vy <- c(vy, 0.3*v)
  }
}
d <- data.frame(x=px, y=py, vx=vx, vy=vy)

# bereid de berekening van contourlijnen voor
f <- function(t,y){ y^3-5*y+t^2-4*t }
t <- seq(-3.5, 7.5, by=0.1)
y <- seq(-4, 4, by=0.1)
dat <- expand.grid(t = t, y = y) # maak een rooster i.v.m. geom_countour
dat <- mutate(dat, z = f(t, y)) # evalueer de functie op elk roosterpunt

# teken het lijnelementenveld met integraalkrommen
ggplot(dat, aes(t, y)) +
  geom_contour(aes(z = z), binwidth=6, colour="blue", size=1) +
  theme(panel.background = element_rect(fill = "white", colour = "grey50")) + 
  geom_segment(data=d, mapping=aes(x=px, y=py, xend=px+vx, yend=py+vy), colour="red") 

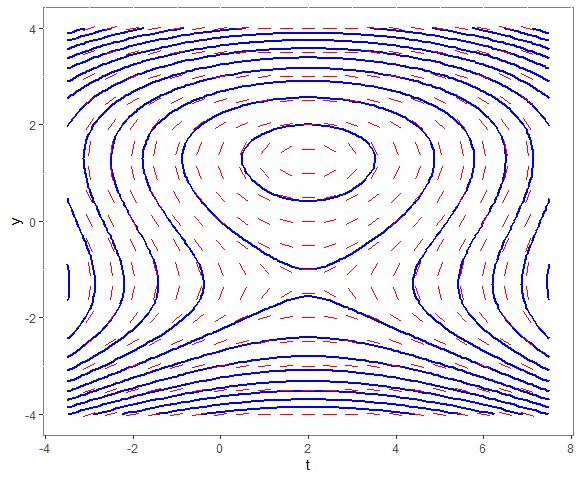
De integraalkrommen beschrijven meer dan één oplossingskromme. De buitenste integraalkromme doet dit voor 3 oplossingskrommen die afhangen van een beginwaarde. We onderscheiden als oplossingskrommen

1. het bovenste deel met \(y\)-waarden groter dan \(\frac{1}{3}\sqrt{15}\);
2. het middelste deel met \(y\)-waarden tussen \(-\frac{1}{3}\sqrt{15}\) en \(\frac{1}{3}\sqrt{15}\);
3. het onderste deel kleiner dan \(-\frac{1}{3}\sqrt{15}\)