Rij- en kolomvectoren en onbestemde vectoren Een vector, die naar gelang het gebruik als rij- of kolomvector worden opgevat, maak je door de getallen op een rijtje te zetten en deze als argument in de concatenatie-functie c te gebruiken. De vector wordt wel als een rijvector getoond in het console venster, maar is het niet echt.

Hieronder staan achter de prompt in een interactieve R sessie opdrachten om een vector te maken. Met de functie array kun je een kolom- of rijvector maken (eigenlijk een matrix met 1 kolom of rij). Een getransponeerde vector wordt verkregen door de functie t te gebruiken.

> v <- c(1,2,3)  # een vector in R zonder dimensie
> v
[1] 1 2 3
> class(v)    # soort object (hoog niveau)
[1] "numeric"
> typeof(v)   # data type van object (laag niveau)
[1] "double" 
> dim(v)
NULL
> rv <- array(v, dim=c(1,3))  # als rijvector
> rv
     [,1] [,2] [,3]
[1,]    1    2    3
> dim(rv)
[1] 1 3
> kv <- array(v, dim=c(3,1)) # als kolomvector 
> kv 
     [,1] 
[1,]    1 
[2,]    2 
[3,]    3 
> t(kv) # getransponeeerde van een kolomvector 
     [,1] [,2] [,3]
[1,]    1    2    3

Dimensie en norm Met de functie dim kun je bepalen of het een rij- of kolomvector is of een dimensieloze vector, maar je kunt er ook de dimensie ook de dimensie van de R-structuur veranderen. Met de functie length kun je het aantal componenten in een vector bepalen. Verwar dit niet met de (Euclidische) lengte van een vector want die bereken je numeriek met de functie norm en er zijn opties om varianten van de norm te berekenen.

> v <- c(4,5,6);  v     # een vector in R zonder dimensie
[1] 4 5 6
> length(v)
[1] 3
> norm(v, type="2") # Euclidische lengte
[1] 8.774964
> dim(v) = c(3,1)   # v nu als kolomvector
> v    
     [,1]
[1,]    4
[2,]    5
[3,]    6
> norm(v, type="2") # Euclidische lengte
[1] 8.774964
> norm(v, type="1") # som van absolute waarden van componenten
[1] 15
> norm(v, type="I") # maximum van absolute waarden van componenten
[1] 6

Speciale constructievormen Verder zijn er speciale commando's om specifieke vectoren te maken; we tonen een paar veel gebruikte constructies, maar er bestaan ook alternatieve commando's.

>> v1 <- 5:11;  v1   # van 5 tot 11
[1]  5  6  7  8  9 10 11   
> v2 <- seq(from=10, to=5, by=-2);  v2    # van 10 tot 5 met stapjes van -2
[1] 10  8  6  
> v3 <- seq(from=0, to=1, length=6);  v3  # gelijkmatige verdeling van 6 punten over [0,1]
[1] 0.0 0.2 0.4 0.6 0.8 1.0 
> v4 <- numeric(3);  v4  # een dimensieloze vector met 3 nullen
[1] 0 0 0 
> v4 <- array(0, 3); v4  # alternatieve constructie
[1] 0 0 0 
> v5 <- array(0, dim=c(3,1));  v5   # kolomvector met 3 nullen
[,1]
[1,] 0
[2,] 0
[3,] 0
> v6 <- logical(3);  v6    #  rijvector met 3 logische waarden  FALSE
[1] FALSE FLASE FALSE
> v7 <- rep(TRUE, 3);  v7  # rijvector met 3 logische waarden TRUE
[1] TRUE TRUE TRUE
> v8 <- c(); v8   # lege vector
NULL
> length(v8)
[1] 0

Aan elkaar plakken van vectoren Je kunt ook nieuwe vectoren creëren door vectoren aan elkaar te plakken met de functie c.

> v1 <- 1:3;  v2 <- 4:6;  v12 <- c(v1, v2);  v12
[1] 1 2 3 4 5 6

Willekeurig gegenereerde vectoren In simulaties zullen we veel gebruik maken van vectoren met willekeurig gegenereerde getallen, in het Engels random numbers genoemd. Hiervoor zijn verschillende instructies:

> runif(5, min=0, max=1)
[1] 0.4422001 0.7989248 0.1218993 0.5609480 0.2065314
> # 10 willekeurige gehele getallen tussen 5 en 8 (inclusief):
> sample(5:8, size=10, replace=TRUE)
[1] 6 6 7 8 6 7 6 7 8 5
> # 5 willekeurige getallen volgens standaard normale verdeling:
> rnorm(5)
[1] -0.2793335 -0.7827303 -0.7789972 -0.3748001 -0.3193938
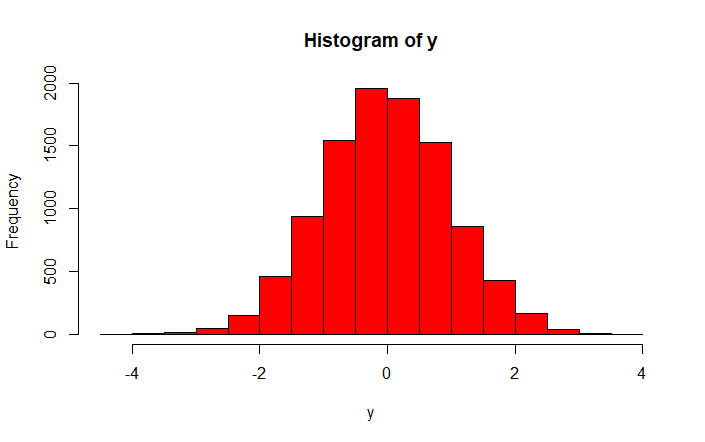
> y <- rnorm(10000)
> hist(y, col="red")