Bij regressieanalyse gaat het om het vaststellen van een verband tussen een afhankelijke variabele \(y\) en één of meer onafhankelijke variabelen. We beperken ons hier tot enkelvoudige lineaire regressieanalyse, dat wil zeggen om een lineair verband \[y=\beta_0+\beta_1x\tiny,\] waarbij \(x\) de onafhankelijke variabele is, en \(\beta_0\) en \(\beta_1\) parameters zijn die zodanig geschat moeten worden dat de rechte lijn het best past bij meetgegevens. Deze lijn noemen we de regressielijn en de bijpassende vergelijking wordt aangeduid met regressievergelijking of regressiemodel.

We maken bij het schatten van de parameters in de regressievergelijking een onderscheid tussen de meetgegevens \((x_1,y_1), \ldots, (x_n,y_n)\) en de geschatte waarden \((x_1,\hat{y}_1), \ldots, (x_n,\hat{y}_n)\) vastgelegd door \[\hat{y}_i=\beta_0+\beta_1x_i\tiny.\] In de kleinste-kwadratenmethode worden waarden van \(\beta_0\) en \(\beta_1\) berekend zodanig dat de som van de kwadratische afwijkingen minimaal is. Met andere woorden, we geven onszelf dan de volgende opdracht \[\text{Minimaliseer }\sum_{i=1}^n(y_i-\hat{y}_i)^2\] De uitkomst is als volgt: \[\begin{aligned} \beta_1 &= \frac{\displaystyle\sum_{i=1}^n (x_i-\bar{x}) (y_i-\bar{y})}{\displaystyle\sum_{i=1}^n (x_i-\bar{x})^2}\\ \\ \beta_0 &= \bar{y}-\beta_1\bar{x}\end{aligned}\] met \[\bar{x}=\frac{1}{n}\sum_{i=1}^nx_i,\quad\text{en}\quad \bar{y}=\frac{1}{n}\sum_{i=1}^ny_i\] Het verschil tussen een gemeten en geschatte waarde, zeg \(\epsilon_i=y_i-\hat{y}_i\), heet een residu. De residuen zeggen iets over de kwaliteit van de regressielijn wat betreft de helling. De gemiddelde gekwadrateerde afwijking, gedefinieerd als \(\displaystyle \frac{1}{n-2}\sum_{i=1}^n \epsilon_i^2\), is een maat voor de kwaliteit van het regressiemodel. Meestal kiest men dan voor de (residuele) standaardafwijking, die gedefinieerd is als de vierkantswortel van de gemiddelde gekwadrateerde afwijking. De standaardafwijking van de schatting van de helling is gelijk aan \[\begin{aligned}\text{sd}(\beta_1) &= \sqrt{\dfrac{1}{n-1}\displaystyle\sum_{i=1}^n \epsilon_i^2}\\[0.25cm] &=\frac{1}{\sqrt{n-1}} \sqrt{\displaystyle\sum_{i=1}^n(y_i-\beta_0-\beta_1x_i)^2}\end{aligned}\] Je kunt ook de correlatiecoëfficiënt tussen de gemeten en geschatte waarden berekenen als indicatie van de kwaliteit van het model.

Enkelvoudige lineaire regressie is gemakkelijk uit te voeren in R met het lm commendo (linear model). Het volgende voorbeeld illustreert dit.

x <- seq(from=0, to=20, by=1)
y <- runif(1, min=1, max=10)+ runif(1, min=0, max=5)*x + 
  rnorm(21, mean=0, sd=1)

# enkelvoudige lineaire regressie
fit <- lm(formula = y ~ x)
print(summary(fit))
# correlatie tussen gegevens en data gegenereerd door lineaire fit
cat("correlatiecoëfficiënt =", cor(y,predict(fit)))

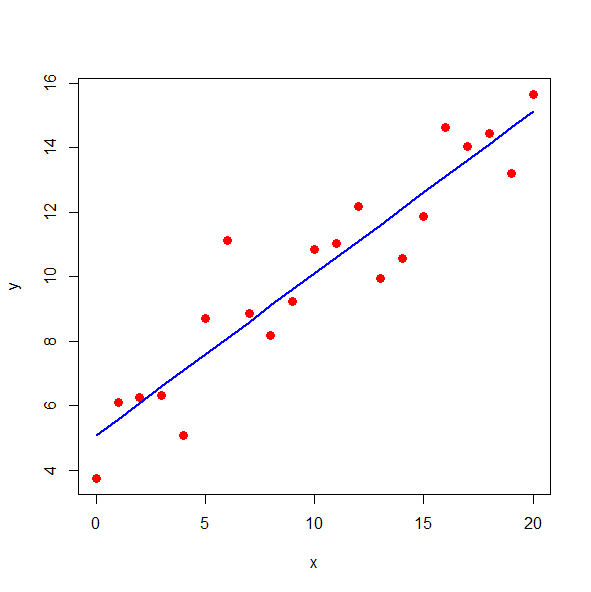
# Visualisatie van data + regressielijn
plot(x, y, type = "p", pch = 16, col = "red", cex = 1.3)
lines(x, predict(fit), type="l", col="blue", lwd=2)

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.0006 -0.9072  0.2761  0.5443  3.0466 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  5.07152    0.53114   9.548 1.10e-08 ***
x            0.50248    0.04543  11.060 1.01e-09 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.261 on 19 degrees of freedom
Multiple R-squared:  0.8656,	Adjusted R-squared:  0.8585 
F-statistic: 122.3 on 1 and 19 DF,  p-value: 1.015e-09

correlatiecoëfficiënt = 0.9303508