Niet-lineaire regressie

Werken met R bij wiskunde: Regressieanalyse in R

Niet-lineaire regressie

We spreken van niet-lineaire regressie zodra modelparameters in een regressiemodel niet lineair voorkomen in de regressievergelijking. Hieronder geven we een overzicht van veelgebruikte niet-lineaire modellen in de context van levenswetenschappen; je kunt ze ook onder andere naamgeving tegenkomen.

\[\begin{array}{|c|c|c|} \hline \textbf{model} & \textbf{formule} & \textbf{opmerking} \\ \hline\\
\text{gegeneraliseerd} & y= \beta_1e^{\beta_2t}+\delta & y(0)=\beta_1+\delta,\\
\text{exponentieel groeimodel} & & \delta\text{ is horizontale asymptoot} \\ \\ \hline\\
\text{gegeneraliseerd} & y= \beta_1\left(1-e^{-\beta_2(t-\delta)}\right) & y(\delta)=0,\\
\text{Mitscherlich groeimodel} & & \beta_1\text{ is horizontale asymptoot}\\ \\ \hline\\
\text{gegeneraliseerd} & y=\dfrac{\beta_1}{1+\beta_2e^{\beta_3t}}+\delta & y(0)=\dfrac{\beta_1}{1+\beta_2}+\delta,\\
\text{logistisch groeimodel} & & \beta_1+\delta\text{ is horizontale asymptoot}\\ \\ \hline\\
\text{Gompertz groeimodel} & y=\beta_1e^{-\beta_2\e^{-\beta_3t}} & \beta_1\text{ is horizontale asymptoot}\\ \\ \hline\\
\text{gegeneraliseerd} & y=\beta_1e^{-\beta_2t}+ \beta_3e^{-\beta_4t}+\delta & \delta\text{ is horizontale asymptoot} \\
\text{bi-exponentieel groeimodel} & & \\ \\ \hline\\
\text{Michaelis-Menten model} & y=\dfrac{\beta_1 x}{\beta_2+x} & \beta_1\text{ is horizontale asymptoot}\\ \\ \hline \\
\text{Hill model} & y=\dfrac{\beta_1 x^\gamma}{\beta_2+x^\gamma} & \beta_1\text{ is horizontale asymptoot}\\ \\ \hline
\end{array}\]

Uitvoering van niet-lineaire regresssie

Er zijn drie manieren om een regressie-analyse van een niet-lineair model uit te voeren:

Transformatie tot een lineair model;
Benadering door een lineair model (linearisatie);
Niet-lineaire regressie via iteratieve methoden zoals bijvoorbeeld de Levenberg-Marquardt methode of de Gauss-Newton methode.

Transformatie naar lineair model Een voorbeeld van transformatie tot een lineair model is het exponentiële groeimodel \[y=\beta_1e^{\beta_2t}\tiny.\] Door transformatie met de natuurlijke logaritme raken we de \(e\)-macht kwijt:\[\ln(y)=\ln(\beta_1) +\beta_2t\tiny.\] We hebben de modelvergelijking nu omgeschreven naar een enkelvoudige lineaire regressie van \(\ln(y)\) versus \(t\).

Het multiplicatie model \(y=\beta_0t^{\beta_1}\) en het S-kromme model \(y=e^{\beta_0+\beta_1/t}\) zijn andere voorbeelden van regressiemodellen die intrinsiek lineair zijn omdat ze door een transformatie met behulp van de natuurlijke logaritme tot een lineair model om te schrijven zijn.

De Michaelis-Menten vergelijking \[y=\dfrac{\beta_1 x}{\beta_2+x}\] is te herschrijven als \[\frac{1}{y}=\frac{\beta_2}{\beta_1}\cdot\frac{1}{x}+\frac{1}{\beta_1}\] en dit impliceert een lineair verband tussen \(\dfrac{1}{y}\) en \(\dfrac{1}{x}\).

Niet-lineaire regressie in R Je kunt in R het nls commando (nonlinear least squares) gebruiken om een niet-lineaire regressie via iteratieve methoden uit te voeren. Als alles mee zit hoef je alleen de formule van het model te specificeren en wordt automatisch een iteratieve oplossingsmethode geselecteerd, maar in veel praktijkgevallen moet je geschikte startwaarden van parameters meegeven en de te gebruiken methode specificeren.

Het volgende gerandomiseerde voorbeeld illustreert het geval dat je geen startwaarden hoeft op te geven bij een niet-lineaire regressie omdat de gebruikte methode toch wel convergeert naar een antwoord (R meldt ook de keuze van de startwaarden).

# genereer parameterwaarden bij model y = b1*x/(b2+x)
b1 <- runif(1, min=1, max=5)
b2 <- runif(1, min=1, max=5)
# maak gegevens met ruis erbij
x <- seq(from=1, to=20, by=1)
y <- (b1*x)/(b2 + x) + rnorm(20, mean=0, sd=0.1)

# voer niet-lineaire regressie uit
nlfit <- nls(formula = y ~ a*x/(b+x))
print(summary(nlfit))

# toon geschatte parameterwaarden in console venster
coeff <- coefficients(nlfit)
cat("a =", coeff[1], ",  b =", coeff[2], "\n")
# toon correlatie tussen gegevens en niet-lineaire fit
cat("correlatiecoëfficiënt =", cor(y,predict(nlfit)), "\n\n")

# visualiseer gegenereerde gegevens en regressiekromme
plot(x, y, type = "p", pch = 16, col = "red", cex = 1.3, 
     main="regressiekromme y = a*x/(b+x)")
lines(x, predict(nlfit), type="l", col="blue", lwd=2)

Bovenstaand R script levert in het console venster het volgende op en levert bijgaand diagram van meetgegevens en regressiekromme.

Formula: y ~ a * x/(b + x)

Parameters:
  Estimate Std. Error t value Pr(>|t|)    
a  2.84716    0.09288  30.653  < 2e-16 ***
b  4.91400    0.49858   9.856 1.12e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.09155 on 18 degrees of freedom

Number of iterations to convergence: 4 
Achieved convergence tolerance: 3.995e-06

a = 2.847156 ,  b = 4.913995 
correlatiecoëfficiënt = 0.9857897

Warning message: 
In nls(formula = y ~ a * x/(b + x)) : 
  No starting values specified for some parameters. 
Initializing ‘a’, ‘b’ to '1.'. 
Consider specifying 'start' or using a selfStart model

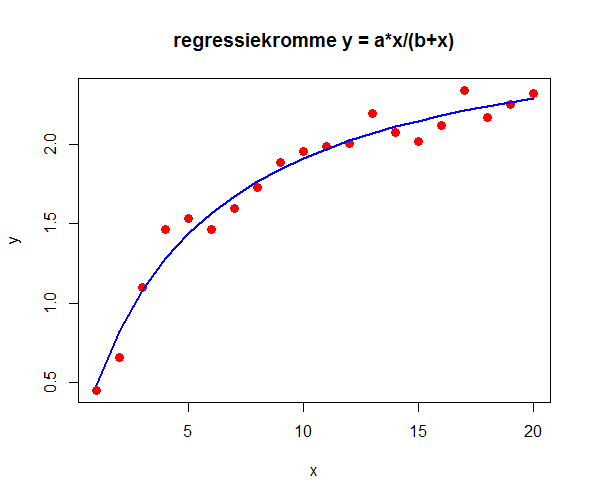
Dit voorbeeld breiden we vervolgens uit om te laten zien dat bij een herschrijving van het niet-lineaire model naar een bijpassend lineair model ook wel een regressiekromme oplevert, maar dat deze toch van mindere kwaliteit is als we de correlatie tussen meetgegevens en modelgegevens als maat hanteren. De parameterwaarden wijken ook behoorlijk af.

# voer transformatie naar lineaire regressie uit
reciproke_x <- 1/x
reciproke_y <- 1/y
# voer lineaire regressie uit
linfit <- lm(formula = reciproke_y ~ reciproke_x)
coeff <- coefficients(linfit)
# bereken parameterwaarden van niet-lineaire fit
alpha <- 1/coeff[1]
beta <- coeff[2]/coeff[1]
# bereken modelgegevens
newfit <- alpha*x/(beta+x)
# toon parameterwaarden in console vester en 
# correlatie tussen gegevens en niet-lineaire fit verkregen
# via transformatie van gegevens
cat("a =", alpha, ",  b=", beta, "\n")
cat("correlatiecoëfficiënt = ", cor(y,newfit), "\n")
# visualiseer gegenereerde gegevens en regressiekromme
plot(x, y, type = "p", pch = 16, col = "red", cex = 1.3, 
     main="regressiekromme y = a*x/(b+x) via transformatie")
lines(x, newfit, type="l", col="blue", lwd=2)

Bovenstaand R script levert in het console venster het volgende op en levert bijgaand diagram van meetgegevens en regressiekromme.

a = 3.011385 ,  b= 5.805604 
correlatiecoëfficiënt =  0.9844066

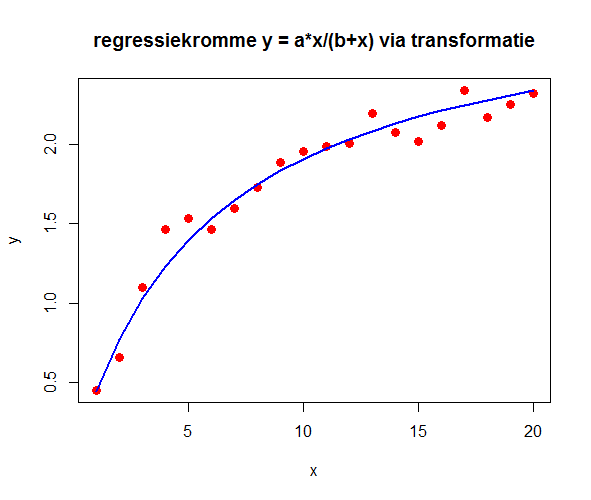
De tweede regressiekromme lijkt op het eerste gezicht op de eerste, maar bij nadere inspectie verschillen ze wel van elkaar en is de kwaliteit van de iteratieve niet-lineaire regressiemethode beter.

Wat we hiervan kunnen leren is dat transformaties van een niet-lineair model naar een lineair model best wel gevaarlijk zijn als het op de kwaliteit van de modeluitkomsten aankomt, maar dat dit wel geschikte startwaarden kan opleveren voor een niet-lineaire regressiemethode