Bi-exponentieel model van bierkraag Elke bierdrinker kent het fenomeen: bij het inschenken van bier in een glas vormt zich een schuimkraag die na verloop van tijd, wanneer het glas onaangeroerd blijft, verdwijnt. De afnemende hoogte van een bierkraag kun je met een bi-exponentieel model redelijk goed wiskundig modelleren. Deze benadering kan als volgt bepaald worden (meetgegeven in csv formaat). Het R script wordt in stappen uitgevoerd.

Stap 1: inlezen en plotten van meetgegevens

# lees gegevens van csv bestand (metingen om de 2 seconde)
gegevens <- read.csv("bierkraag.csv", header = TRUE,
                     sep = ";", dec = ".", na.strings="", fill = TRUE)
t <- gegevens$tijd    # tijd in sec
H <- gegevens$hoogte  # hoogte bierkraag in cm
# teken gegevens in een scatterplot
plot(t, H, type="p", pch=1, cex=0.7, col="red",
     xlab="t (in sec)", ylab="hoogte (in cm)", 
     main="Hoogte van bierkraag versus tijd")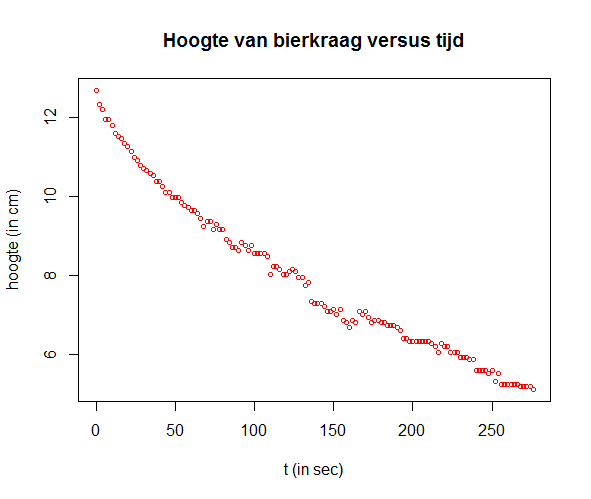

Stap 2: beschrijven van het tweede deel van meetgegevens met exponentiële regressie

Als je een exponentieel groeimodel aannemelijk vindt, kun je dit verifiëren door de logartime van de grootheid uit te zetten tegen de tijd omdat dit dan een rechte lijn moet opleveren. In dit specifieke geval zie je dan dat na verloop van tijd, zeg als \(t>30\), inderdaad een rechte lijn de logaritme van de hoogte goed beschrijft. Op dit geselecteerde stukje kun je dan het exponentiële groeimodel toepassen.

Onderstaand R script levert de niet-lineaire functiefit en een bijpassend diagram op.

# zet ln(H_data) uit tegen t_data
plot(t, log(H), type="p", pch=1, cex=0.7, col="red",
     xlab="t", ylab="ln(H)", 
     main="ln(H) versus t")
# selecteer gegevens na 30 seconden
selectie <- c(t.data>30)
ts <- t[selectie]
Hs <- H[selectie]
lnHs <- log(Hs)
# lineaire regressie met ln(Hs) als lineaire functie van t
fit <- lm(formula = lnHs ~ ts)
lines(ts, predict(fit), type="l", col="blue", lwd=2)

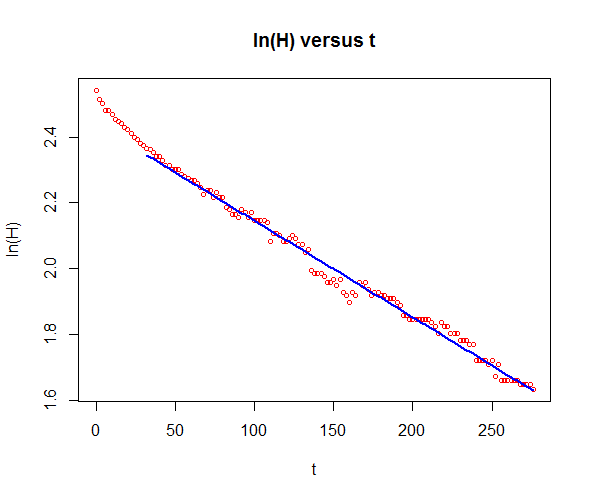
We tekenen vervolgens de meetgegeven en het exponentiële groeimodel.

# teken gegevens in een scatterplot en voeg expontiële fit toe
coeffs <- coefficients(fit)
a1 <- exp(coeffs[1])
r1 <- coeffs[2]
H_fit <- a1*exp(r1*t)
plot(t, H, type="p", pch=1, cex=0.7, col="red",
     xlab="t (in sec)", ylab="hoogte (in cm)", 
     main="Hoogte versus tijd met exponentieel model")
lines(t, H_fit, type="l", col="blue", lwd=2)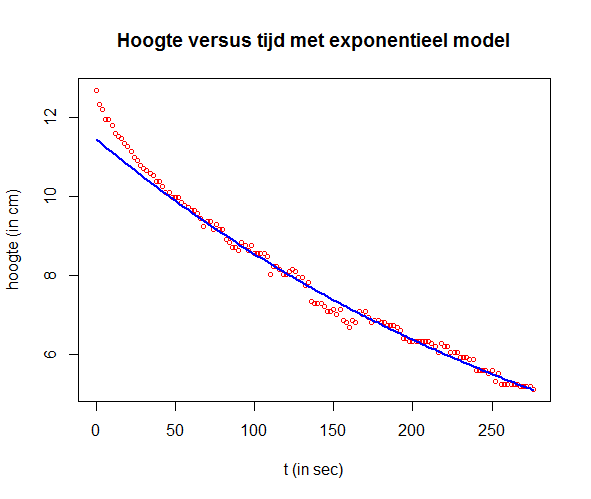

Stap 3: plotten van residuen

De regressiekromme beschrijft de meetgegevens in het begin nog niet goed, maar dat is niet zo belangrijk. Waar het om gaat is dat de residuen opnieuw een exponentieel verval karakter vertonen. Onderstaand R script laat dit zien.

# bereken residuen en teken de grafiek hiervan
residuen <- H - H_fit
plot(t, residuen, type="p", pch=16, cex=0.7, col="red",
     xlab="t (in sec)", ylab="residu (in cm)", 
     main="residuen versus tijd")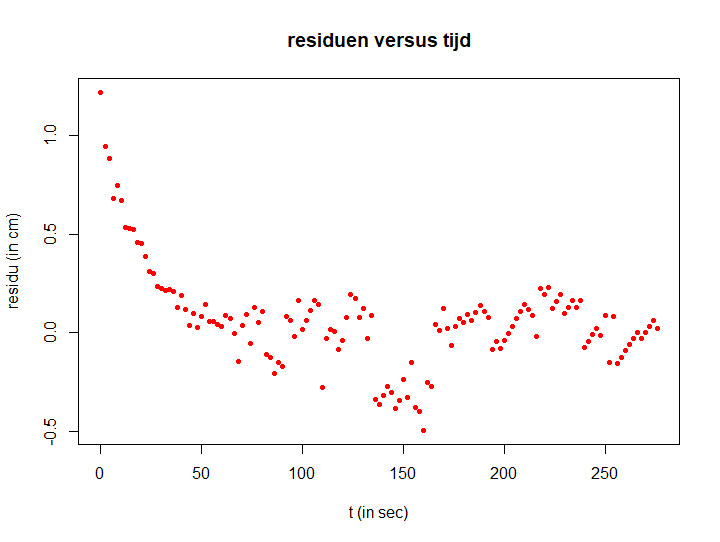

Stap 4: beschrijven van eerste deel van residuen met opnieuw exponentieel model

We kunnen op dezelfde manier als eerst een exponentieel model voor het eerste deel van de residuen berekenen. Voor de verandering doen we eens een niet-lineaire fit met een schatting van startwaarden van de parameters via de methode van partiële sommen. Onderstaand R script levert de exponentiële fit van de residuen en een bijpassend diagram op.

# selecteer gegevens in eerste minuut
selectie <- c(t<60)
ts <- t[selectie]
Rs <- residuen[selectie]
# doe parameterschatting via partiële sommen
N <- 15
dt <- 2
s1 <- sum(Rs[1:N])
s2 <- sum(Rs[N+1:30])
r <- (log(s2)-log(s1)) / (N*dt)
h <- exp(r*dt)
a <- s1 * (1-h) / (1-h^N)
# voer niet-lineaire regressie uit
nlfit <- nls(formula = Rs ~ a_2*exp(r_2*ts), 
             start = list(a_2=a, r_2=r))
coeffs <- coefficients(nlfit)
a2 <- coeffs[1]
r2 <- coeffs[2]
R_fit <- a2*exp(r2*t)
# teken residuen in een scatterplot en voeg expontiële fit toe
plot(t, residuen, type="p", pch=16, cex=0.7, col="red",
     xlab="t (in sec)", ylab="residu (in cm)", 
     main="residuen versus tijd met exponentieel model")
lines(t, R_fit, type="l", col="blue", lwd=2)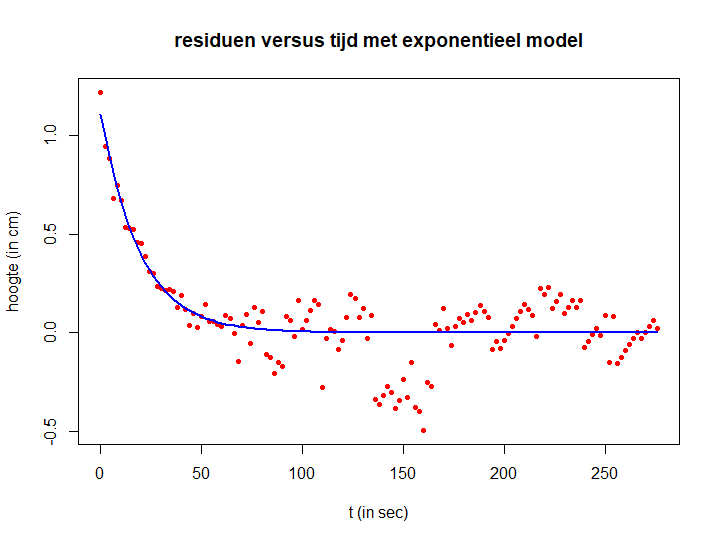 

Stap 5: alles bij elkaar zetten

Tellen we de beide berekende regressiekrommen op dan hebben we een niet-lineaire regressie van de gemeten hoogte van de bierkraag in de loop van de tijd:

# totaalresultaat
plot(t, H, type="p", pch=1, cex=0.7, col="red",
     xlab="t (in sec)", ylab="hoogte (in cm)", 
     main="Hoogte van bierkraag versus tijd plus bi-exponentieel model")
lines(t, H_fit + R_fit, type="l", col="blue", lwd=2)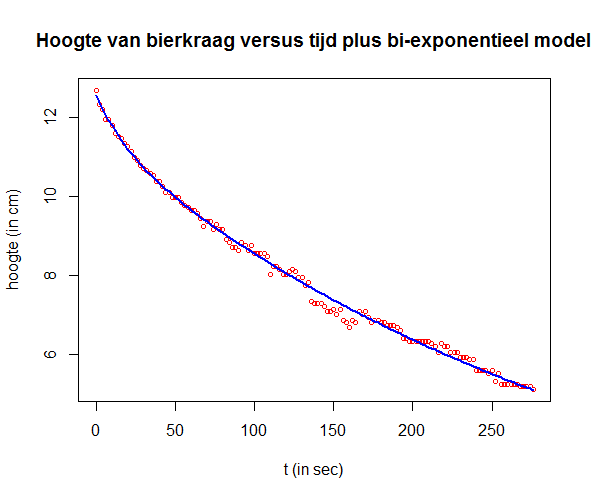

Stap 6: Niet-lineaire regressie met uiteindelijke model en reeds gevonden parameterschattingen

Nog beter is het om de gevonden parameterwaarden te gebruiken als startwaarden voor het volgende regressiemodel \[\text{hoogte} = a_1\cdot e^{r_1\cdot t}+ a_2\cdot e^{r_1\cdot t}\] Onderstaand R script doet het werk.

# uiteindelijke niet-lineaire regressie:
# voer exponentiële regressie met twee componenten uit
nlfit <- nls(formula = H ~ a.1*exp(r.1*t) + a.2*exp(r.2*t),
             start = list(a_1=a1, r_1=r1, a_2=a2, r_2=r2))
print(summary(nlfit))  # print resultaten
# teken de meetgegevens en de regressiekromme
plot(t, H, type="p", pch=1, cex=0.7, col="red",
     xlab="t (in sec)", ylab="hoogte (in cm)", 
     main="Hoogte van bierkraag versus tijd plus bi-exponentieel model")
lines(t, predict(nlfit), type="l", col="blue", lwd=2)
# bereken de correlatie tussen gegevens en modelresultaten 
cat("correlatiecoëfficiënt =", cor(H,predict(nlfit)))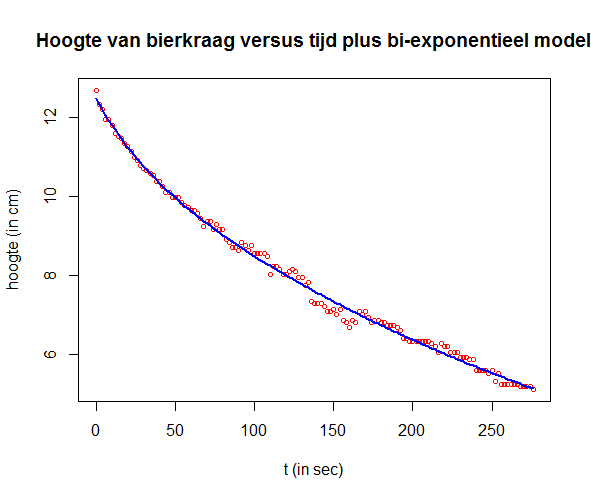

De uiteindelijke parameterschattingen staan hieronder getabelleerd. Ook is de correlatiecoëfficiënt tussen meetgegevens en modelresultaten berekend en afgedrukt. Het eindresultaat is van goede kwaliteit!

Formula: H ~ a_1 * exp(r_1 * t) + a_2 * exp(r_2 * t)

Parameters:
      Estimate Std. Error t value Pr(>|t|)    
a.1  1.121e+01  1.119e-01 100.191  < 2e-16 ***
r.1 -2.822e-03  5.164e-05 -54.641  < 2e-16 ***
a.2  1.284e+00  1.087e-01  11.815  < 2e-16 ***
r.2 -3.338e-02  5.665e-03  -5.892 2.89e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1399 on 135 degrees of freedom

Number of iterations to convergence: 8 
Achieved convergence tolerance: 7.89e-06

correlatiecoëfficiënt = 0.9975641

Kniehoek tijdens lopen: harmonische analyse De kniehoek van een meisje is gemeten tijdens wandelen met constante snelheid op een loopband. De bewering is dat deze hoek heel aardig te beschrijven is als som van twee sinusoïden. Dit is een voorbeeld van harmonische analyse. Deze benadering kan als volgt bepaald worden. Het R script wordt in stappen uitgevoerd.

Stap 1: inlezen en plotten van meetgegevens

# lees gegevens van csv bestand
gegevens <- read.csv("kniehoekmetingen.csv", 
  header = TRUE, sep = ";", dec = ".", na.strings="", 
  fill = TRUE)
t <- gegevens$tijd    # tijd in sec
hoek <- gegevens$kniehoek  # kniehoek in graden
# teken gegevens in een scatterplot
plot(t, hoek, type="p", pch=16, cex=0.7, col="red",
     xlab="t (in sec)", ylab="kniehoek (in graden)", 
     main="kniehoek versus tijd ")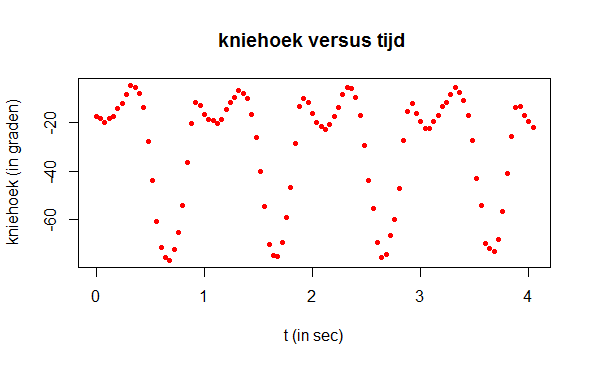

Stap 2: beschrijven van meetgegevens met sinusoïdale regressie

Dit lijkt op een periodiek beweging met een frequentie van ongeveer 1 s^-1. We benaderen de meetgegevens eerst maar eens met een enkelvoudig sinusoïdaal regressiemodel \[\text{hoek} = a_1\sin(b_1t+c_1)+d_1\] waarbij de sinusfunctie argumenten in graden opvat. Hiervoor moeten we in R een sinusfunctie in graden definiëren. We schatten de startwaarden van de parameters voor een niet-lineaire regressiemethode als volgt:

• uit de frequentie volgt een schatting voor de startwaarde van \(b_1\), namelijk: \(b_1=360\);
• de amplitude \(a_1\) krijgen we als de helft van het verschil tussen uiterste hoekwaarden;
• de verticale verschuiving \(d_1\) van de sinusoïde schatten we in als de gemiddelde hoekwaarde want het tijdsinterval lijkt uit vier perioden te bestaan;
• de fasehoek schatten we, bij gebrek aan beter, in eerste instantie gelijk aan 0.

Onderstaand R script levert de niet-lineaire functiefit en een bijpassend diagram op.

# definieer sinus functie in graden ipv radialen als input 
sin_in_graden <- function(graden) {
  radialen <- graden*(pi/180)
  return(sin(radialen))
}
# voer sinusoïdale regressie uit
fit1 <- nls( formula = hoek ~ a1 * sin_in_graden(b1 * t + c1) + d1, 
            start=list(a1=(max(hoek) - min(hoek)) / 2, 
                       b1=360, c1 = 0, d1=mean(hoek)))
coeffs1 <- coefficients(fit1)
a1 <- coeffs1[1]
b1 <- coeffs1[2]
c1 <- coeffs1[3]
d1 <- coeffs1[4]
hoek1 <- a1 * sin_in_graden(b1 * t + c1) + d1
# teken meetgegevens en regressiekromme
plot(t, hoek, type="p", pch=16, cex=0.7, col="red",
     xlab="t (in sec)", ylab="kniehoek (in graden)", 
     main="kniehoek versus tijd plus sinusoïde")
lines(t, hoek1, type="l", col="blue", lwd=2)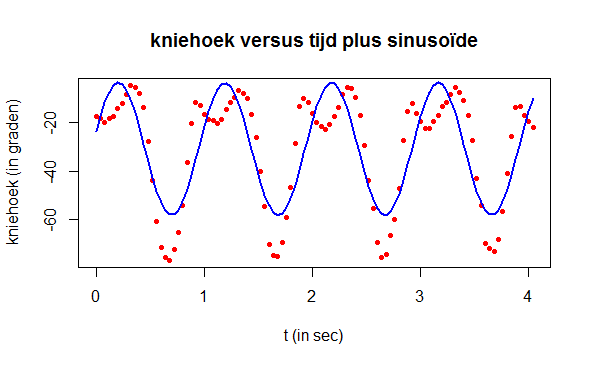

Stap 3: plotten van residuen

De regressiekromme beschrijft de meetgegevens niet goed, maar dat is niet zo belangrijk. Waar het om gaat is dat de residuen opnieuw een periodiek karakter vertonen. Onderstaand R script laat dit zien.

# bereken residuen en teken de grafiek hiervan
residuen <- hoek - hoek1
plot(t, residuen, type="p", pch=16, cex=0.7, col="red",
     xlab="t (in sec)", ylab="residu (in graden)", 
     main="residuen versus tijd")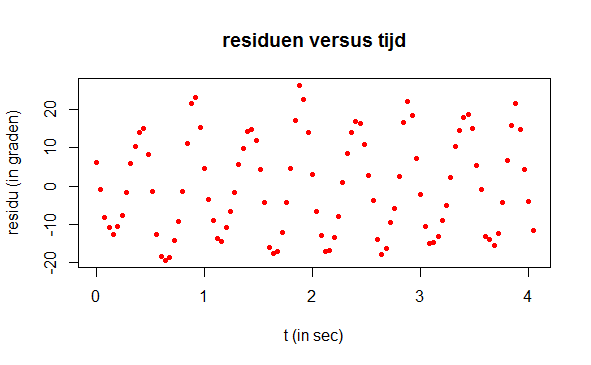

Stap 4: beschrijven van residuen met opnieuw sinusoïdale regressie

Dit lijkt op een periodiek beweging met een frequentie van ongeveer 2 s^-1. We benaderen de residuen eerst maar eens met een enkelvoudig sinusoïdaal regressiemodel \[\text{hoek} = a_2\sin(b_2t+c_2)+d_2\] waarbij de sinusfunctie argumenten in graden opvat. We schatten de startwaarden van de parameters voor een niet-lineaire regressiemethode als volgt:

• uit de frequentie volgt een schatting voor de startwaarde van \(b_2\), namelijk: \(b_1=720\);
• de amplitude \(a_2\) krijgen we als de helft van het verschil tussen uiterste waarden van residuen;
• de verticale verschuiving \(d_1\) van de sinusoïde schatten we in als dicht bij 0. We nemen dus \(d_2=0\);
• Kijkend naar de grafiek lijkt het op een tegengestelde van een sinus. Dit gegeven brengt ons op het idee om te schatten \(c_2=180\) (overeenkomend met \pi\)).

Onderstaand R script levert de niet-lineaire functiefit van de residuen en een bijpassend diagram op.

# voer sinusoïdale regressie uit
fit2 <- nls( formula = residuen ~ a2 * sin_in_graden(b2 * t + c2) + d2, 
             start = list(a2=(max(residuen) - min(residuen)) / 2, 
                          b2=720, c2=180, d2=0))
coeffs2 <- coefficients(fit2)
a2 <- coeffs2[1]
b2 <- coeffs2[2]
c2 <- coeffs2[3]
d2 <- coeffs2[4]
hoek2 <- a2 * sin_in_graden(b2 * t + c2) + d2
# teken residuen en regressiekromme
plot(t, residuen, type="p", pch=16, cex=0.7, col="red",
     xlab="t (in sec)", ylab="residu (in graden)", 
     main="residuen versus tijd plus sinusoïde")
lines(t, hoek2, type="l", col="blue", lwd=2)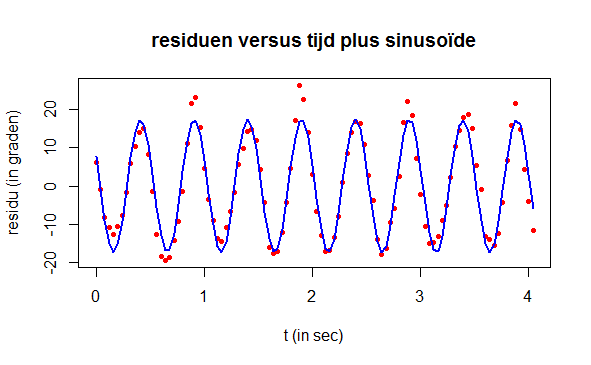

Stap 5: alles bij elkaar zetten

Tellen we de beide berekende regressiekrommen op dan hebben we een niet-lineaire regressie van de gemeten kniehoeken tijdens het lopen:

# totaalresultaat
plot(t, hoek, type="p", pch=16, cex=0.7, col="red", ylim=c(-80,0),
     xlab="t (in sec)", ylab="kniehoek (in graden)", 
     main="kniehoek versus tijd plus regressiekromme")
lines(t, hoek1 + hoek2, type="l", col="blue", lwd=2)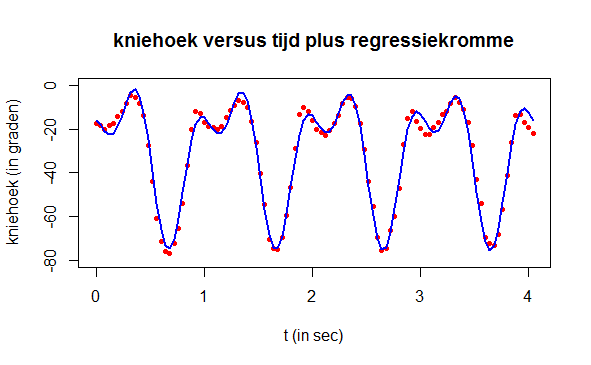

Stap 6: Niet-lineaire regressie met uiteindelijke model en reeds gevonden parameterschattingen

Nog beter is het om de gevonden parameterwaarden te gebruiken als startwaarden voor het volgende regressiemodel \[\text{hoogte} = a_1\sin(b_1t+c_1)+a_2\sin(b_2t+c_2)+d\] Onderstaand R script doet het werk.

# uiteindelijke niet-lineaire regressie:
# voer sinusoïdale regressie met twee sinusfuncties uit
nlfit <- nls(formula = hoek ~ 
               a_1 * sin_in_graden(b_1 * t + c_1) + 
               a_2 * sin_in_graden(b_2 * t + c_2) + 
               d,
             start = list(a_1=a1, b_1=b1, c_1=c1, 
                          a_2=a2, b_2=b2, c_2=c2, 
                          d=d1))
print(summary(nlfit))  # print resultaten
# teken de meetgegevens en de regressiekromme
plot(t, hoek, type="p", pch=16, cex=0.7, col="red", ylim=c(-80,0),
     xlab="t (in sec)", ylab="kniehoek (in graden)", 
     main="kniehoek versus tijd plus regressiekromme")
lines(t, predict(nlfit), type="l", col="blue", lwd=2)
# bereken de correlatie tussen gegevens en modelresultaten 
cat("correlatiecoëfficiënt =", cor(hoek,predict(nlfit)))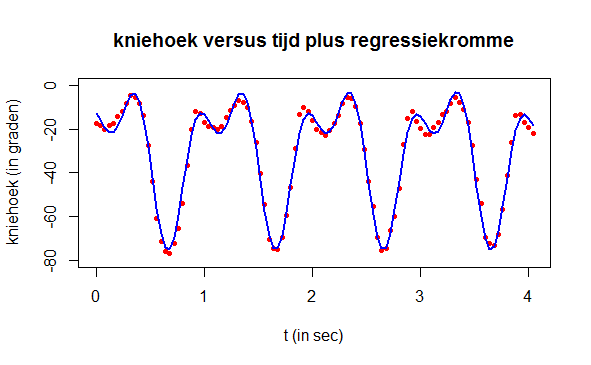

De uiteindelijke parameterschattingen staan hieronder getabelleerd. Ook is de correlatiecoëfficiënt tussen meetgegevens en modelresultaten berekend en afgedrukt. Het eindresultaat is van hoge kwaliteit!

Formula: hoek ~ a_1 * sin_in_graden(b_1 * t + c_1) + a_2 * sin_in_graden(b_2 * 
    t + c_2) + d

Parameters:
    Estimate Std. Error t value Pr(>|t|)    
a_1  27.2705     0.4548   59.96   <2e-16 ***
b_1 361.0197     0.8135  443.76   <2e-16 ***
c_1  23.1223     1.9446   11.89   <2e-16 ***
a_2  17.7445     0.4588   38.68   <2e-16 ***
b_2 723.3587     1.2204  592.72   <2e-16 ***
c_2 155.6522     2.8692   54.25   <2e-16 ***
d   -30.7267     0.3206  -95.83   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.22 on 95 degrees of freedom

Number of iterations to convergence: 4 
Achieved convergence tolerance: 5.11e-06

correlatiecoëfficiënt = 0.9908715