Doing mathematics with R: Differential equations in R
 Solving a first order initial value problem
Solving a first order initial value problem
There are several R packages to deal with differential equations. We will primarily use the deSolve package as it provides the most commonly applicable working environment. You need to install this package in R Studio or R with all dependent packages included and then it can be made available in a session as follows:
> library("deSolve")Of course it makes sense to look at the examples on the website http://desolve.r-forge.r-project.org/ and see examples. A good reference is the textbook Solving Differential Equations in R of the Soetaert, Cash & Mazzia. In this section we only discuss the basics.
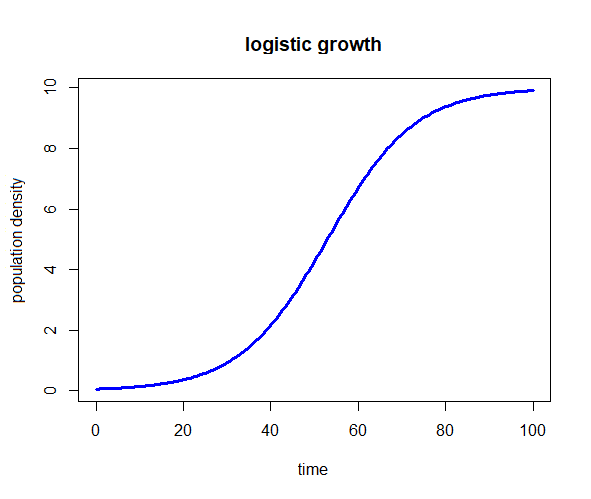
Below we give the logistic growth model as an example. Study this carefully because all the following examples follow the structure chosen here.
The logistic growth model Let's look at the initial value problem \[\frac{\dd y}{\dd t}=r\cdot y\cdot (1-y/K), \quad y(0)=y_0\] We specify the initial value problem in the form of an R function with the following three arguments:
- the independent variable, where we usually choose time \(t\);
- the initial state of the dependent variable, in this case the quantity \(y\);
- parameters, which here are the parameters \(r\) and \(K\).
The function returns a list of derivatives, but in this case it is just \(\frac{dy}{dt}\), and is used in the numerical method to solve the differential equation. In the code snippet below, the statement with(as.list(c(initialstate, parameters)). ...) ensures that the names of the parameters are available in the definition of the differential equation.
model <- function(time, initialstate, parameters){
with(as.list(c(initialstate, parameters)), {
dydt <- r*y*(1-y/K)
return(list(dydt))
})
}As initial value, parameter values, and the time interval, we successively choose:
y0 <- c(y=0.05) # inital value of population density
params <- c(r=0.1, # relative growth rate r
K=10) # carrying capacity K
t <- seq(from=0, to=100, by=0.5) # time intervalThe growth model is now solved with the ode instruction:
solution <- ode(y0, t, model, params)The output is an object containing an array that tabulates the values of the dependent variable at specified times. You can use this to draw a graph of the solution curve. If you want to know more about how the initial value problem is solved numerically, use the diagnostics(solution) instruction.
plot(solution, col="blue", main="logistic growth",
xlab="time", ylab="population density", lwd=3)produces the following diagram: