Het logistische groeimodel We bekijken het beginwaardeprobleem \[\frac{\dd y}{\dd t}=r\cdot y\cdot (1-y/K), \quad y(0)=y_0\] We specificeren het beginwaardeprobleem in de vorm van een R functie met de volgende drie argumenten:

• de onafhankelijke variabele, waarbij wij meestal tijd \(t\) kiezen;
• de begintoestand van de afhankelijke variabele, waarbij het hier de grootheid \(y\) betreft;
• parameters, waarbij het hier om de parameters \(r\) en \(K\) gaat.

De functie levert een lijst van afgeleiden op, maar in dit geval is het enkel \(\frac{dy}{dt}\), en wordt gebruikt in de numerieke methode om de differentiaalvergelijking op te lossen. In onderstaand code fragment zorgt de instructie with(as.list(c(begintoestand, parameters)). ...) ervoor dat de namen van de parameters beschikbaar zijn in definitie van de differentiaalvergelijking.

model <- function(tijd, begintoestand, parameters){
  with(as.list(c(begintoestand, parameters)), {
    dydt <-  r*y*(1-y/K)
    return(list(dydt))
  })
}

Als beginwaarde, parameterwaarden, en het tijdsinterval kiezen we achtereenvolgens:

y0 <- c(y=0.05)    # beginwaarde van populatiedichtheid 
params <- c(r=0.1, # relatieve groeisnelheidsconstante r
            K=10)  # draagkracht K
t <- seq(from=0, to=100, by=0.5)  # tijdsinterval

Het groeimodel wordt nu opgelost met het ode commando:

oplossing <- ode(y0, t, model, params)

De uitvoer is een object met hierin een matrix die de waarden van de afhankelijke variabele bij opgegeven tijdstippen tabelleert. Je kunt hiermee een grafiek van de oplossingskromme tekenen. Wil je meer weten over hoe het beginwaardeprobleem numeriek precies is opgelost, toets dan het commando diagnostics(oplossing) in.

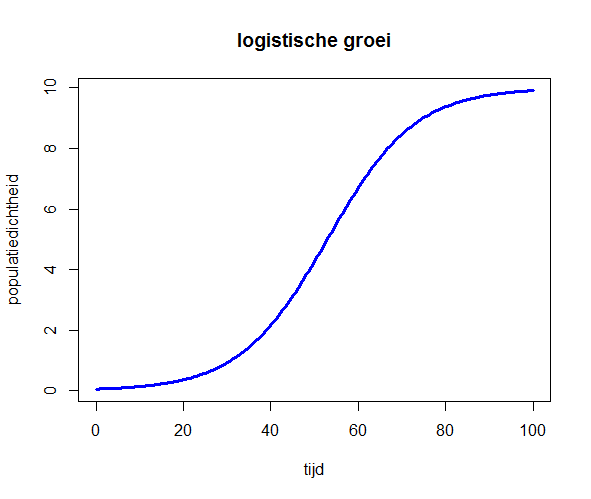
plot(oplossing, col="blue", main="logistische groei", 
     xlab="tijd", ylab="populatiedichtheid", lwd=3)

levert onderstaand diagram op: